Thermodynamics of Batteries

There is no denying that batteries play a critical role in our modern world. Powering everything from small electronic devices to electric vehicles and renewable energy storage systems. Understanding the underlying thermodynamics of batteries is essential for optimizing their performance, efficiency, and longevity. This article explores the fundamental principles of thermodynamics as they apply to batteries. Delving into the processes that govern energy storage. By examining the thermodynamic processes at play within battery cells, we can gain valuable insights into how to improve battery technology. As the demand for reliable energy storage solutions grows so will the understanding of batteries.

What does thermodynamically metastable mean?

Thermodynamically metastable refers to a state in which a system is in a phase that requires overcoming an energy barrier to transform into a phase of lower free energy. This temporary phase is characterized by unstable conditions and uncontrolled energy levels, often leading to system failures. Despite being unstable, the metastable phase is the system’s final and most stable state. It usually represents the lowest possible energy levels.

Many batteries are considered thermodynamically metastable. This is because one or both electrodes have an electric potential that falls outside the electrolyte’s potential stability range. This implies that the electrolyte molecules must oxidize and/or reduce either the anode or the cathode, respectively.

Why are Thermodynamic techniques and methods important when it comes to batteries?

Thermodynamic techniques and methods are valuable for understanding the behavior of anodes, cathodes, and full lithium-ion batteries (LIBs). During various stages such as charge, discharge, overcharge, and cycle aging. A battery cell is made of an anode, a cathode that reversibly integrates lithium ions into their host structures, following a general schematic equation:

H+xLi⁺+xe⁻⇌Li_x​H_i​

where ( x ) represents the electrode and/or cell reaction advancement rate (0 ≤ x ≤ 1). The change in the cell’s Gibbs free energy ΔG(x) is related to the cell’s open-circuit potential (OCP) ( E⁰(x) ) as:

ΔG(x) = nFE⁰(x)

where ( n ) is the number of transferred ions (here, ( n = 1 ) for ( Li⁺ )) and ( F ) is Faraday’s constant. The cell potential at equilibrium ( E^0(x) ) is defined as:

E⁰(x)=E₀^+​(x)−E₀⁻​(x)

where (E⁺₀(x) ) and ( E^–₀(x) ) denote the cathode and anode potentials, respectively. ΔG(x) also relates to changes in enthalpy ΔH(x) and entropy ΔS(x) at a defined electrode composition as:

ΔG(x)=ΔH(x)−TΔS(x)

Electrode Interface Explained

In a cell, reactions primarily occur at two specific areas known as electrode interfaces. In simple terms, the reaction at one electrode (reduction in the forward direction) can be depicted as

aA + ne = cC

where molecules of A take up n electrons e to form c molecules of C

At the other electrode, the reaction (oxidation in the forward direction) can be represented by

bB – ne = dD

The overall reaction in the cell is given by the addition of these two half-cell reactions

aA + bB = cC+ dD

The alteration in the standard free energy G0 of this reaction is represented by the equation:

ΔG⁰=−nFE⁰

where:

• n is the number of electrons transferred per reaction,
• F is the Faraday constant (96,485.4 coulombs),
• E⁰ is the standard electromotive force (voltage)

What is the Nernst equation and what does it explain?

It describes how an electrode’s potential depends on its chemical environment. More precisely, the Nernst Equation indicates the potential of an electrode when it is in a solution containing a redox-active species, considering the activities of both its oxidized and reduced forms.

When the conditions differ from the standard state, the voltage 𝐸 of a cell is determined by the Nernst equation, which is:

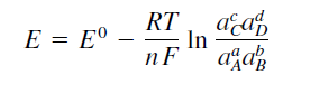
where:

• 𝐸⁰ is the standard cell potential,
• 𝑅 is the gas constant,
• 𝑇 is the absolute temperature,
• 𝑛 is the number of moles of electrons transferred,
• 𝐹 is the Faraday constant,
• 𝑄 is the reaction quotient.

The alteration in the standard Gibbs free energy ΔG⁰ of a cell reaction is the driving force that allows a battery to provide electrical energy to an external circuit.

Thermodynamic quantities of a Battery

Thermodynamic quantities in a battery can be classified as either extensive or intensive, based on how they relate to the size or amount of the battery. Extensive quantities depend on the size or amount of material in the system, while intensive quantities are independent of the system’s size or amount.

Thermodynamics of Batteries: Extensive Quantities:

• Mass of the battery: The mass of the battery is an extensive quantity because it increases with the size of the battery.
• Capacity of the battery (C): The capacity of the battery, measured in ampere-hours (Ah), is also an extensive quantity because it represents the total amount of charge the battery can store, which depends on its size.
• Enthalpy: Enthalpy, a measure of the total energy of a system, is an extensive quantity because it depends on the amount of material in the system.

Thermodynamics of Batteries: Intensive Properties:

• Temperature: Temperature is an intensive property because it does not depend on the size of the battery. It is a measure of the average kinetic energy of the particles in the system.
• Open Circuit Voltage (OCV): OCV is the voltage of the battery when no current is flowing. It is an intensive property because it does not depend on the size of the battery.
• Specific Energy: Specific energy is the energy stored per unit mass of the battery. It is an intensive property because it is independent of the size of the battery.
• Specific Heat (per kg): Specific heat is the amount of heat required to raise the temperature of one kilogram of a substance by one degree Celsius. It is an intensive property because it does not depend on the amount of material.
• Heat Capacity (per mole): Heat capacity is the amount of heat required to raise the temperature of one mole of a substance by one degree Celsius. It is an intensive property because it is independent of the amount of material.

In summary, extensive quantities of a battery, such as mass, capacity, and enthalpy, depend on the size or amount of material in the system. In contrast, intensive properties, such as temperature, OCV, specific energy, specific heat, and heat capacity, are independent of the size or amount of the battery. Understanding these distinctions is crucial for analyzing and designing efficient battery systems for various applications.

How to calculate the specific energy of the battery?

To calculate the specific energy of a battery, you can use the formula:

Specific Energy (Wh/kg)=Specific Capacity (Ah/kg)×Cell Voltage (V)

The specific energy is the total amount of electrical energy stored by a battery per unit of mass. It is typically measured in watt-hours per kilogram (Wh/kg).

Here, the Specific Capacity is the capacity of the battery per unit mass, usually measured in ampere-hours per kilogram (Ah/kg), and the Cell Voltage is the voltage of the battery cell.

Therefore, to calculate the specific energy, you multiply the specific capacity by the cell voltage. This calculation gives you the amount of energy the battery can store per unit of mass.

Example Problem

calculate the specific energy of the following reaction.

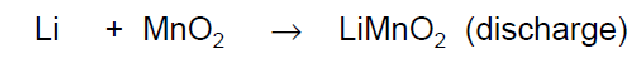
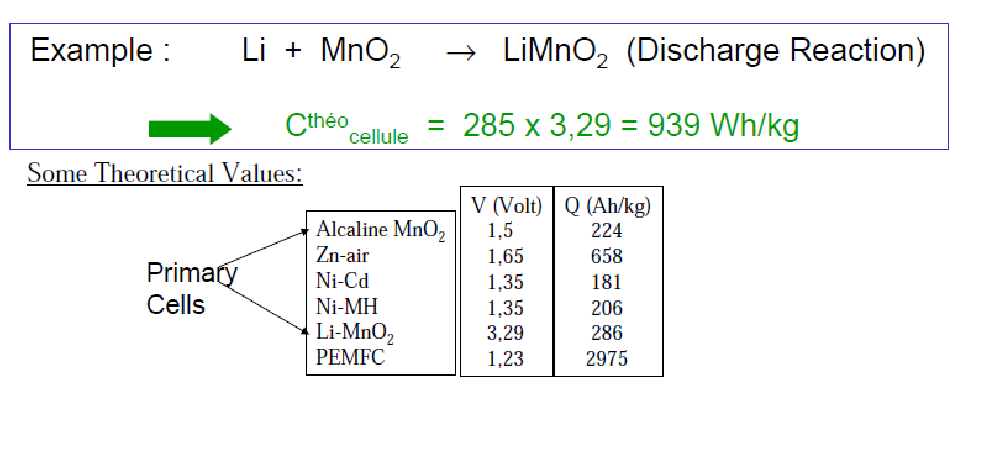
solution

One electron: -1.602*10-19C
One Li-Atom mass: 6.94/(6.02 × 1023 )g
One MnO2 mass: 86.9/(6.02 × 1023 )g

Therefore in order to transfer Q=1.602*10-19C charge, we will need the overall mass M=(6.94+86.9)/(6.02 × 1023 )g So the theoretical specific capacity of this battery is Q/M

How do you calculate specific capacity?

To calculate the specific capacity of a battery, you can use the formula:

Specific Capacity (Ah/kg)=Energy Capacity (Wh)​/Cell Voltage (V)×Mass of the battery (kg)

The specific capacity is the total amount of electrical charge stored by a battery per unit of mass. It is typically measured in ampere-hours per kilogram (Ah/kg).

Here, the Energy Capacity is the total energy stored by the battery, usually measured in watt-hours (Wh), the Cell Voltage is the voltage of the battery cell, and the Mass of the battery is the total mass of the battery.

To calculate the specific capacity, divide the energy capacity by the product of the cell voltage and the mass of the battery. This calculation gives you the amount of charge the battery can store per unit of mass.

Why is high energy density (or specific energy) of such interest?

High energy density, or specific energy, is of great interest because it allows for longer device run times per unit volume or weight of the battery. This means that a battery with higher energy density can provide the same performance as a lower energy density battery but with lower volume or weight.

For portable electronic devices, electric vehicles, and other applications where space and weight are critical factors, high-energy-density batteries are essential. They enable devices to be more compact and lighter without sacrificing performance, leading to improved portability and efficiency.

How do you achieve high specific energy?

Achieving high specific energy in a battery involves several key strategies:

1. High Capacity Electrode Materials: Using electrode materials with high capacity for storing and releasing ions or electrons can increase the overall energy storage capacity of the battery. Materials such as lithium cobalt oxide (LiCoO2) for cathodes and graphite for anodes are commonly used in lithium-ion batteries due to their high specific capacities.
2. High Voltage Electrode Materials: Using electrode materials with higher voltage potential can increase the energy output of the battery. For example, lithium iron phosphate (LiFePO4) has a lower voltage compared to lithium cobalt oxide but is safer and has a longer lifespan, making it a suitable choice for certain applications.
3. Lightweight Components: Using lightweight materials for components such as current collectors, separators, and casing can reduce the overall weight of the battery without compromising its performance. This can lead to higher specific energy as the battery can store more energy per unit weight.

By combining these strategies, researchers and engineers can design batteries with higher specific energy, allowing for longer-lasting and more efficient energy storage solutions.

Conclusion

In conclusion, understanding the thermodynamics of batteries is crucial for developing efficient and sustainable energy storage solutions. By delving into the intricate processes at the electrode interfaces and the overall cell behavior during different stages of operation, researchers can enhance battery performance, lifespan, and safety. Thermodynamic principles offer valuable insights into the complex interplay of factors that govern battery operation, paving the way for the development of advanced battery technologies that meet the growing demands of our energy landscape.