Magnetism, Permanent Magnets, and Solenoids
Magnetism is one of the most fascinating phenomena in physics, shaping how we interact with the world and power our modern technologies. From the invisible forces that guide compasses to the intricate designs of electromagnets and permanent magnets, magnetism plays a pivotal role in various scientific and industrial applications.
Among the many tools that harness magnetic forces, solenoids are versatile electromechanical devices with a wide range of uses, from fluid control systems to robotics. This article explores the fundamentals of magnetism, delves into the properties of permanent magnets, and uncovers the diverse applications of solenoids, shedding light on the magnetic forces that drive innovation.
The Magnetic Field from a Moving Point Charge
A moving charge creates a magnetic field (B), as described by the equation:
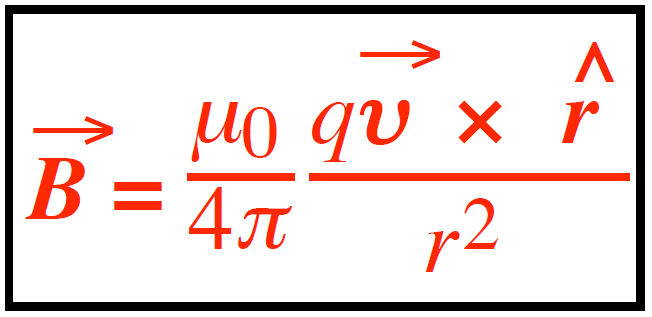
Where:
- B is the magnetic field (in T)
- μ0 is the permeability of free space (4π×10−7 Tm/A).
- q is the charge in coulombs (C, where 1 C ≡ 1 A·s).
- v is the constant velocity of the charge (in m/s).
- r is the distance (in m) between the source point (the point charge) to the field point.
- r^ is a unit vector directed from the source point to the field point. A unit vector has no unit but has magnitude one (unity).
The magnitude of the field depends on the angle (ϕ) between the charge’s velocity and the vector r^:
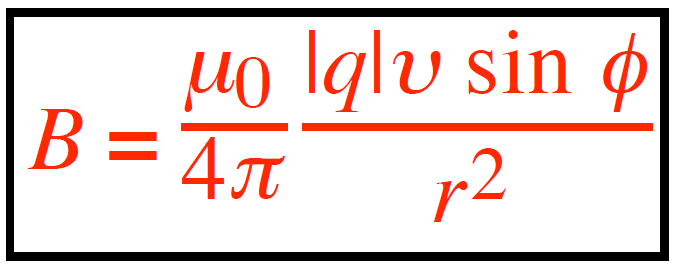
Where:
φ is the angle between the directions of υ and r^.
What is the law of Biot Savart?
The Biot-Savart law states that the magnetic field generated by a current-carrying conductor at a specific point is inversely proportional to the square of the distance between the conductor and the point. Additionally, the magnetic field is directly proportional to the conductor’s length and the current flowing through it. This law extends the concept of a magnetic field to currents. For a tiny length of current (dl):
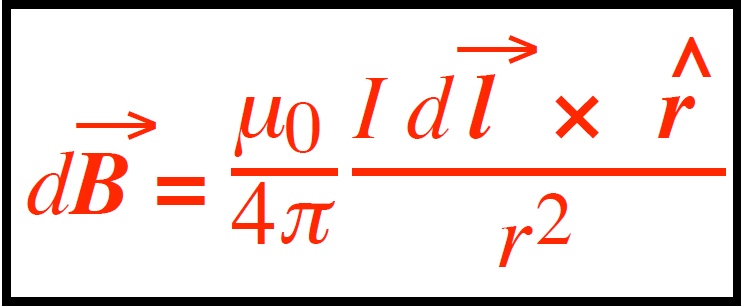
Where:
- dB is an infinitesimal magnetic field (in T) caused by a current I (in A).
- dL is infinitesimal length (in m).
- r is the distance (in m) from the source point (the infinitesimal length dl) to the field point.
- r^ is the corresponding unit vector.
This law explains phenomena such as:
Magnetic fields around long straight wires: B=μ0I/2πr , where r is the distance from the center of the wire to the field point.
Right-hand rule: Curl your fingers around the wire in the direction of the current; with your extended thumb in the direction the current flows. Your fingers then wrap around in the direction of the magnetic field (B). Parallel currents attract, but antiparallel (opposite) currents repel.
Magnetic Fields in Circular Coils
For a flat circular coil with N turns and radius a, the magnetic field along its axis is given by:
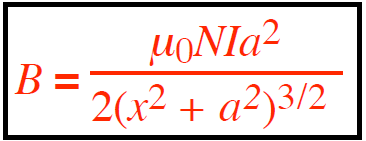
where x is the distance (in m) along the axis from the center of the coil to the field point and a is the coil’s radius (in m). At the center (x=0), the field simplifies to:
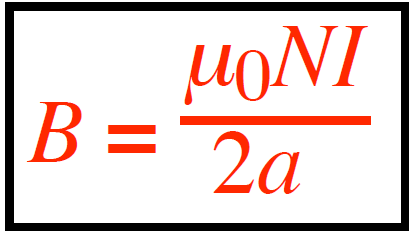
The direction of the magnetic field (B) aligns with the magnetic dipole moment and area vectors. You can use the right-hand rule to find the direction of the magnetic field lines.
What is the Ampere’s law?
Ampere’s law states that the magnetic field generated by an electric current is directly proportional to the magnitude of the current, with the proportionality constant being the permeability of free space. Ampere’s Law relates the magnetic field around a closed loop to the current enclosed by that loop:

where Iencl is the net constant current (in A) enclosed by the path of the integral. This law is particularly useful for highly symmetrical systems, such as solenoids and toroids:
Solenoid
A solenoid is a helical coil wrapped in a cylinder. When its length is much greater than its diameter, a uniform magnetic field near its center: is B=μ0nI, where n is the number of turns per unit length (in m–1).
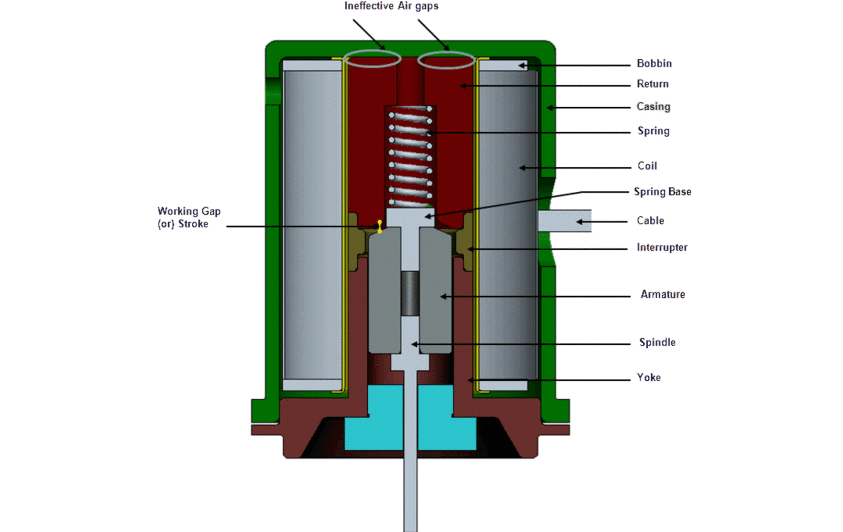
Purpose of a Solenoid
A solenoid functions as an electromagnet and an actuator, converting electrical energy into mechanical motion for diverse applications. A solenoid generates a magnetic field by passing an electric current through its coil, making it a versatile device in various scientific, industrial, and mechanical contexts.

Application of a Solenoid
One primary use of solenoids is as electromagnets, where their ability to create a controlled magnetic field is leveraged in scientific experiments, educational tools, and applications requiring strong magnetic fields.
Another critical function is as actuators, where solenoids translate electrical energy into mechanical motion. This is accomplished by displacing a ferromagnetic plunger, enabling the operation of mechanical systems such as valves, switches, and levers.
In fluid control, solenoids are integral to pumps and valves, offering precise control over fluid flow, and making them essential in industrial and everyday systems. Their robustness also allows them to excel in high-endurance applications, such as aerospace environments near aircraft engines, where their compact design generates high force and withstands harsh conditions.
Additionally, solenoids are employed in robotics and mechanical systems to generate impacts or impulses and are used in scientific research to study magnetic fields, such as in laser-plasma experiments. Solenoids are invaluable for their multifunctionality, offering precise, reliable, and efficient operation across various applications.
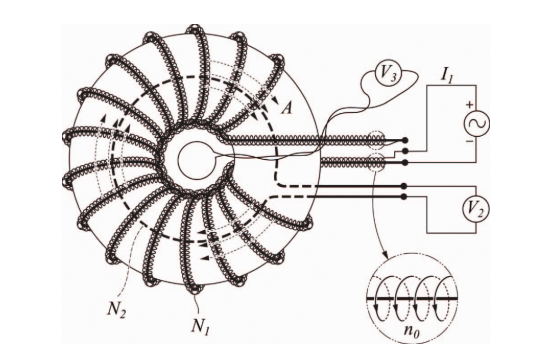
What is a toroid solenoid?
A toroid solenoid is a type of solenoid where the coil is wound around a toroidal (doughnut-shaped) core. This configuration has several unique characteristics and applications. A doughnut-shaped coil has a magnetic field which can be found using the following equation:
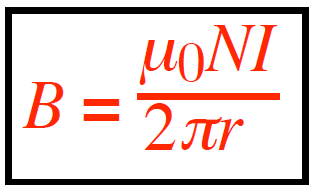
N is the number of turns (no unit) and r is the distance (in m) from the center to the field point. This B is the magnitude of the tangential magnetic field (in T) in the “dough” of the doughnut-shaped core (that is, within the turns). The magnetic field is primarily confined within the core in a toroid solenoid, creating a closed-loop magnetic path. This is in contrast to a straight solenoid where the magnetic field extends outside the coil
Application of a Solenoid
Due to their efficient magnetic field containment and reduced EMI, Toroid solenoids are used in various applications, including transformers and inductors. They are also used in specialized metamaterials to achieve unique electromagnetic properties such as negative refraction and backward waves
Magnetization and Magnetic Materials
The magnetic dipole moments of atoms are caused mainly by the orbital and spin motions of their electrons (nuclear magnetism is about 103 times smaller), which can align in the presence of an external magnetic field.
What is a paramagnetism in physics?
Paramagnetism is the temperature-dependent lining up of the atomic magnetic dipoles when placed in an external magnetic field. The paramagnetic behavior decreases with increasing temperature as thermal agitation disrupts the alignment of magnetic moments. In the material, except at very low temperatures, paramagnetism gives only a slight increase over the external magnetic field value.
Paramagnetic materials have a small, positive susceptibility to magnetic fields, meaning a magnetic field slightly attracts them but does not retain the magnetic properties when the external field is removed. This is due to the presence of some unpaired electrons and the realignment of the electron paths caused by the external magnetic field.
What is diamagnetic with an example?
Diamagnetism is a property of materials that are repelled by a magnetic field. When exposed to an external magnetic field, these materials create an induced magnetic field in the opposite direction, resulting in a repulsive force. Unlike paramagnetic and ferromagnetic materials, which are attracted to magnetic fields, diamagnetic substances consistently exhibit this repulsion.
Bismuth, known for its strong diamagnetic properties, is an example of a diamagnetic material. Other examples include silver, gold, carbon, zinc, marble, water, and antimony. Notably, diamagnetism is a universal property found in all materials and is unaffected by temperature.
What is ferromagnetism in simple words?
Ferromagnetism is a physical phenomenon where certain electrically neutral materials exhibit a strong attraction to others. This type of magnetism can be found in iron, cobalt, nickel, and certain alloys or compounds that include one or more of these elements. In ferromagnetism, adjacent atomic magnetic dipoles line up in strong parallelism in regions called magnetic domains. In unmagnetized ferromagnetic material, those domains have random orientations.
An external magnetic field causes those domains to grow and/or rotate to give a large magnetization. Ferromagnetic materials exhibit hysteresis, a phenomenon where the material retains magnetization even after the external field is removed.
How are ferromagnetic materials classified, and what factors affect their magnetism?
Ferromagnetic materials are categorized into two types: soft magnetic materials, such as annealed iron, which do not retain magnetization, and hard magnetic materials, like alnico, which are ideal for creating permanent magnets. The magnetism in these materials arises from the alignment of electron spins, and this alignment typically diminishes with increased temperature.
Permanent Magnets and Hysteresis
Hysteresis loops demonstrate how magnetic domains behave under varying magnetic fields. Permanent magnets result from domains that remain aligned even after the external field is removed. These materials are crucial in applications like data storage and electric motors.
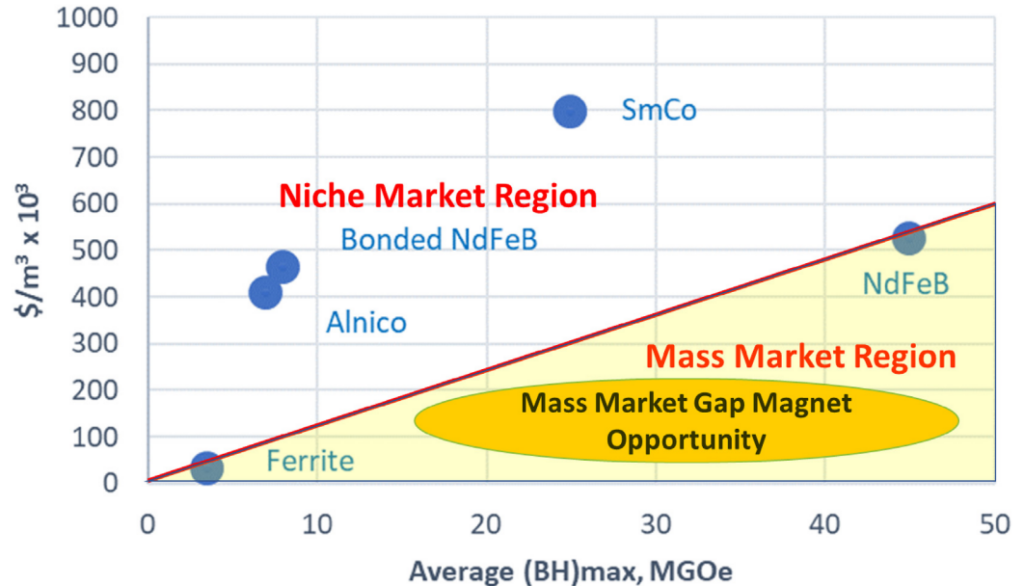
What are the five permanent magnets?
The five main types of permanent magnets, each with unique properties and applications, are:
- Sintered Neodymium-Iron-Boron (Nd-Fe-B):
Due to their excellent magnetic properties, fully dense magnets are widely used in various applications. They are known for their high magnetic strength. - Bonded Neodymium-Iron-Boron (Nd-Fe-B):
Made by bonding Nd-Fe-B powder with a polymer, these magnets offer flexibility in shape and size but have lower magnetic strength compared to sintered Nd-Fe-B. - Ferrite (Ceramic Magnets):
Composed primarily of iron oxide mixed with barium or strontium carbonate, ferrites are cost-effective, corrosion-resistant, and suitable for applications where high magnetic performance is not critical. - Samarium Cobalt (Sm-Co):
These rare earth magnets are known for their high magnetic strength and excellent thermal stability, making them ideal for high-temperature applications. - Aluminum Nickel Cobalt (Alnico):
Alnico magnets, made from aluminum, nickel, and cobalt, offer good temperature stability and are widely used in industrial applications.
These magnets are selected based on key properties like maximum energy product, coercivity, remanence, and maximum working temperature, which determine their suitability for specific applications.
What factors should be considered when selecting a permanent magnet for an application?
Permanent magnets, made from “hard” ferromagnetic materials like alnico, are integral to modern technology and are widely used in devices such as electromagnets, electric motors, and generators.
Key Magnetic Properties:
When selecting a permanent magnet for an application, it is crucial to evaluate key magnetic properties to ensure optimal performance. These properties include the maximum energy product (BH)max, which indicates the magnet’s energy density and potential for generating a magnetic field. Coercivity (Hc), which measures resistance to demagnetization by external fields.
Intrinsic coercivity (HCi or HCj), reflects the ability to resist irreversible demagnetization. Other essential properties are remanence (Br), representing the residual magnetic strength after removing the external field, and the maximum working temperature, which defines the temperature range within which the magnet retains its properties. These characteristics provide a general baseline for assessing magnet performance.
Magnet Grades:
Magnets are further categorized into grades that reflect their performance under specific conditions. Each grade is typically represented by a number (indicating maximum energy product) and letter(s) (denoting maximum operating temperature). This classification allows for precise alignment with application requirements, as the grade determines how a magnet performs under varying temperature-dependent conditions. Therefore, selecting the correct grade is just as important as choosing the appropriate magnet type.
Magnet Type and Group:
Another critical factor is the type of magnet used in an application. Permanent magnets, such as Nd-Fe-B, Sm-Co, ferrite, and Alnico, each offer unique properties and are suited for different uses. For example, some magnets excel in high-temperature environments, while others are more cost-effective for applications where high magnetic performance is not essential. Carefully matching the magnet type to the application’s demands ensures functionality and efficiency.
Economic Considerations:
Finally, economic considerations must be taken into account when selecting a magnet. High-performance magnets often come at a higher cost, and not all applications require the most advanced options. Balancing the desired magnetic properties and performance with economic constraints ensures the selected magnet is both effective and cost-efficient for the intended purpose. By addressing these factors comprehensively, the most suitable permanent magnet for any application can be identified.
Conclusion
Understanding magnetic fields and their interactions with charges and materials is fundamental to physics and engineering. From the microscopic movements of electrons to macroscopic applications like motors and transformers, these principles drive innovation in technology and energy.
Whether you’re grasping the right-hand rule or exploring Ampere’s Law, these concepts serve as stepping stones toward mastering the complex world of electromagnetism.






You have mentioned very interesting points! ps nice web site.