Vehicle Dynamics of EVs
In the rapidly evolving landscape of automotive technology, electrified vehicles have taken center stage, promising a cleaner, more sustainable future for transportation. As we embrace the shift towards electric mobility, understanding the intricacies of vehicle dynamics and energy management becomes paramount. Among the many factors influencing the efficiency of electrified vehicles, vehicle longitudinal dynamics plays a pivotal role.

The field of vehicle dynamics involves examining the motion of a vehicle, specifically how its forward movement evolves in reaction to factors such as driver inputs, outputs from the propulsion system, and the prevailing ambient and road conditions.
Why Longitudinal Vehicle Dynamics Matter in Energy Management
Longitudinal vehicle dynamics involve the study of a vehicle’s motion along its length – how it accelerates, decelerates, and maintains speed. When it comes to vehicle energy consumption, the powertrain system and the longitudinal vehicle dynamics are typically considered. The lateral dynamics is typically neglected as it does not have a major impact on vehicle’s energy consumption. However, the lateral motion control is extremely important for vehicle stability. In the realm of electrified vehicles, where every watt-hour matters, comprehending these dynamics becomes crucial for optimizing energy usage.

When discussing vehicle dynamics and energy management, it is crucial to consider the influence of the driver. An aggressive driver can induce substantially higher net forces on the vehicle, affecting its performance and velocity in response to various parameters.
Unveiling the Vehicle Motion Equation
At the heart of longitudinal vehicle dynamics lies the vehicle motion equation, a complex interplay of forces that determines how a vehicle moves. This equation is dirived from Newton’s second law (F=MA). One key player in this equation is tractive force. The traction force 𝐹𝑡 is the force generated by the prime mover minus the force that is used to accelerate the rotating parts inside the vehicle and minus all friction losses in the powertrain. In other words the traction force is the force generated by the vehicle’s propulsion system. In an BEV, this force is often supplied by electric motors driven by batteries while in a gas powered vehicle it would be by the engine and transmission.

Sample Problem: Vehicle Dynamics of Electrified Vehicles
Consider a vehicle with mv = 1500kg, A · Cd = 0.7m2, μ = 0.012, a vehicle speed v = 120km/h and an
acceleration a = 0.027g.
(i) Calculate the traction torque required at the wheels and the corresponding rotational speed level:
tire radius rw = 0.317m.
(ii) Calculate the road slope that is equivalent to that acceleration.

Forces at Play in Automotive Vehicle Dynamics: Aerodynamic Drag and Rolling-Resistance
As the vehicle accelerates, it encounters two formidable adversaries: aerodynamic drag force and rolling resistance force. Aerodynamic drag results from air resistance, demanding more energy as the vehicle’s speed increases. Aerodynamic drag force depends on: Frontal Area 𝐴𝑓, drag coefficient 𝐶𝐷, air density 𝜌𝑎, and vehicle velocity 𝑣.

Understanding Rolling-resistance and tires
The tire stands out as the pivotal component in a vehicle, playing a decisive role in determining overall vehicle dynamics. Extensive research in the realm of vehicle dynamics focuses on the construction and responses of tires to various loads. The way tires behave under different types of loads—be it vertical, lateral, or longitudinal—directly influences the overall behavior of the vehicle.

Stiffer tires exhibit improved responsiveness but are less effective at dampening vibrations. On the other hand, softer tires, while offering superior isolation capabilities, lack responsiveness to load changes, leading to compromised handling. Wider tires enhance traction and grip, albeit at the expense of increased rolling resistance.
Rolling-resistance, is the friction between the tires and the road, sapping energy with every rotation. On hard surfaces, Rolling-resistance is caused primarily by deformation of the tire. The pressure in the leading half is larger than the trailing half of the contact surface, resulting in a torque against the movement of the vehicle.
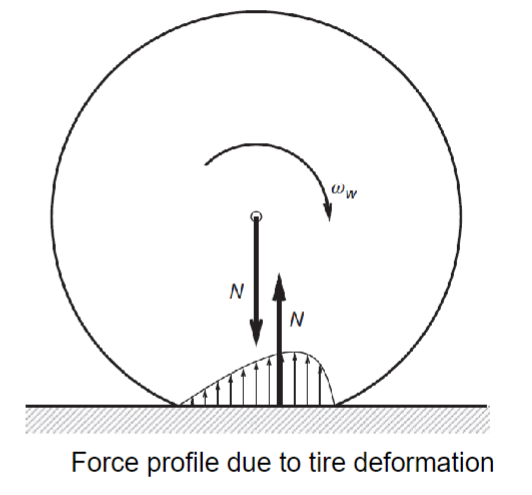
Rolling-resistance is often modeled using the following equation:
𝐹𝑟 = 𝜇 (𝑣, 𝑝, …)⋅ 𝑚𝑣 ⋅ 𝑔 ⋅ cos𝛼
The most important influencing factors are vehicle speed 𝑣, tire pressure 𝑝, road surface conditions and vehicle mass 𝑚𝑣. The rolling resistance coefficient is assumed:
- constant, independent of vehicle velocity,
- have both linear and constant component based on observation: rolling resistance does generally change with vehicle speed, and the assumption of a linear form is a reasonable approximation.
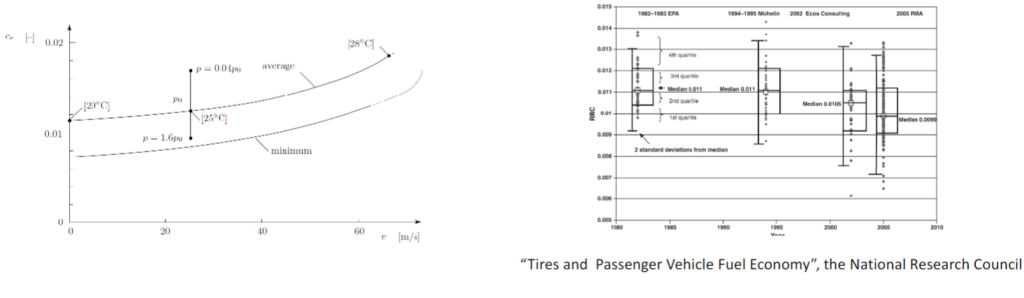
The tire model stands out as the most challenging and vulnerable aspect to simulate accurately. It is crucial for the tire model to accurately simulate realistic shear forces across various scenarios, including braking, acceleration, cornering, and their combinations, while accounting for diverse surface conditions.
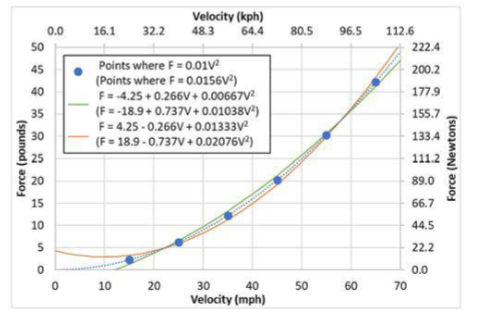
Decoding Coastdown Road Load Coefficients
Coastdown road load coefficients are akin to the fingerprints of a road on a vehicle’s efficiency. They encapsulate the unique resistance a vehicle faces when coasting to a stop. By understanding and optimizing these coefficients, engineers can fine-tune the vehicle’s performance to extract maximum efficiency.
The vehicle is accelerated to a speed above 71.5 mph (115 kph), the transmission is shifted into neutral, and data are taken as the vehicle coasts down until the vehicle speed drops below 9.3 mph (15 kph). Time and speed data are collected during the coastdown and are used to determine a force-versus speed road load expression. Road load is assumed to be second-order: 𝐹𝑡𝑜𝑡𝑎𝑙 = 𝐹0 + 𝐹1𝑣 + 𝐹2𝑣2 . The losses that this test captures are Aerodynamic losses, Tire rolling losses, Driveline losses, and Minor losses.
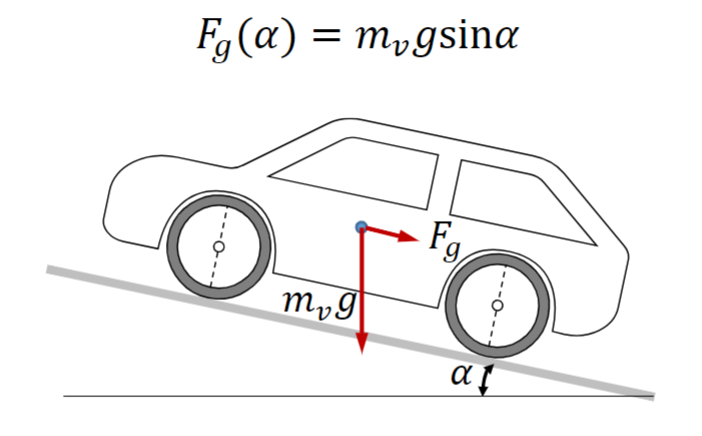
The Gravitational Challenge
As vehicles navigate slopes and hills, gravitational force comes into play. Ascending requires more energy input to counteract the gravitational pull, while descending presents an opportunity for regenerative braking – converting the potential energy gained during the climb back into usable energy.
The force induced by gravity is modeled by the relationship: 𝐹𝑔(𝛼) = 𝑚𝑣𝑔sin𝛼. For small inclinations, 𝐹𝑔(𝛼) = 𝑚𝑣𝑔𝛼.
Inertial Forces: The Need for Smart Transitions
Inertial forces come into play during accelerations and decelerations. Efficient energy management requires a delicate balance – too much acceleration may drain the battery, while abrupt decelerations waste the energy generated during motion.
The inertia of the vehicle and of all rotating parts inside the vehicle causes fictitious (d’Alembert) forces.
𝑚𝑣 𝑑𝑣/𝑑𝑡 = 𝐹𝑡(𝑡) − 𝐹𝑎(𝑡) + 𝐹𝑟(𝑡) + 𝐹𝑔(𝑡) + ⋯
The inertia of the rotating masses of the powertrain can be taken into account in the respective sub-models. Sometimes, for rapid calculation, it may be convenient to add the inertia of the rotating masses to the vehicle mass.

Performance and Drivability: Striking the Right Balance
Longitudinal Vehicle dynamics directly impact the perceived performance and drivability of an electrified vehicle. Balancing acceleration, braking, and overall responsiveness becomes an art, ensuring that the driver’s experience aligns with the efficiency goals of the vehicle. For passenger cars, three main quantifiers are often used:
- Top speed;
- Maximum gradeability;
- Acceleration time from standstill to a reference speed (100km/h or 60mph)
The Nexus of Longitudinal Vehicle Dynamics and Energy Management
How do these dynamics collectively affect the energy management of electrified vehicles? Imagine a ballet of forces, with engineers orchestrating the delicate dance between tractive force and the opposing forces of drag, resistance, and gravity. Efficient energy management requires a nuanced understanding of when to supply power, when to recuperate energy, and how to optimize transitions between these states.
As electrified vehicles continue to gain prominence, manufacturers are investing heavily in cutting-edge technologies to enhance longitudinal dynamics. Advanced control algorithms, regenerative braking systems, and smart energy management systems are becoming the linchpin of electric vehicle development.
Conclusion
In conclusion, the journey towards efficient electrified vehicles is a multifaceted one, where longitudinal dynamics emerge as the guiding star. For readers with intermediate technical knowledge, delving into the nuances of tractive forces, coastdown coefficients, and gravitational challenges unlocks the gateway to a deeper understanding of energy management. As we pave the way for a greener future on our roads, the mastery of longitudinal dynamics stands as a testament to our commitment to harnessing the full potential of electrified vehicles.