Electrical Flux and Gauss’s Law

In physics, the study of electric fields and their interactions with matter is fundamental to understanding how electric charges influence their surroundings. This article is going to dive into two crucial concepts in electromagnetism: Electric Flux and Gauss’s Law. These concepts play an essential role in analyzing and solving problems related to electric fields and charge distributions. Let’s break them down and explore their key ideas in detail.

What is Electrical Flux?

Electric flux is a measure of the electric field passing through a given surface. It provides a way to quantify the effect of an electric field on a surface area. Alright, imagine you’re at the Niagara Falls watching water go over the falls. You know how you can measure the amount of water passing through a particular area in a given time interval.

Based on that you are able to multiple it by the length of the falls to calculate how much water goes over the falls per unit time. Well, in a similar way, electrical flux is like measuring the flow of electric field lines passing through a given surface.

Simply put, electrical flux tells us how much electric field is “flowing” through a given surface. It’s like a sneak peek into the invisible forces surrounding charged particles. The cool thing is, it depends on how the surface is oriented with respect to the electric field – so, if you rotate the surface, you’ll get different flux values.

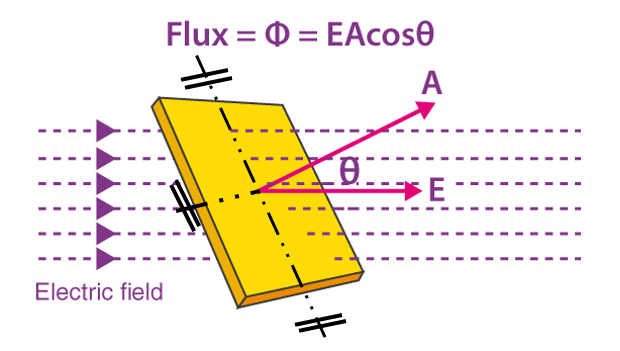
How is electric flux used?

The electric flux Φ_E through a surface is related to electric field lines passing through a closed surface. It helps calculate the net charge enclosed within the surface by Gauss’s law and is valuable in analyzing electric fields around charged objects, such as capacitors, and understanding the behavior of electric fields in different situations.

Although we can draw as many electric field lines as we want to represent the electric field, electric flux has a definite value. If E is uniform (that is, constant in magnitude and direction) and a flat area A is perpendicular to E then,

Special Cases of Electric Flux

The units for eletric flux Φ_E are in Nm² / C

• Uniform Electric Field Perpendicular to Surface : If the electric field is uniform and perpendicular to a flat surface, the flux is simply the product of the electric field (E) and the area (A): Φ_E​=E⋅A
• Electric Field at an Angle : When the electric field is at an angle to the surface (as shown in the pictures below), the flux is reduced by the cosine of the angle between the electric field and the normal to the surface: Φ_E​=E⋅A⋅cosϕ

In this case, the electric flux becomes E⊥​A, where E⊥​ is the component of the electric field that is perpendicular to the surface.

Flux Through a Closed Surface

For closed surfaces, the flux is defined as: Φ_E​=∫E⋅dA

Where the area vector dA is always outwardly normal to the surface.

Does electric flux depend on angle?

Yes, electric flux depends on the angle between the electric field lines and the surface area of the closed surface. When the electric field lines are perpendicular to the surface, the electric flux is maximized. In contrast, if the lines are parallel or at an angle, the flux decreases accordingly. If E is uniform over a flat area A, with an angle φ then Φ_E​=E⋅A⋅cosϕ.

Where:

• E is the electric field vector.
• A is the area vector of the surface.
• Φ is the angle between the electric field and the surface normal.

Using E cos φ = E⊥,

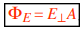
Also, using EA cos φ = E·A,

That area vector A has a magnitude A (in m²) and a direction normal (that is, perpendicular) to the surface. For closed surfaces, A and dA are always outwardly normal to the surface. E⊥ is the component of E perpendicular to the surface (and parallel to A or dA ). φ is the angle between the directions of the vectors E and A or dA .

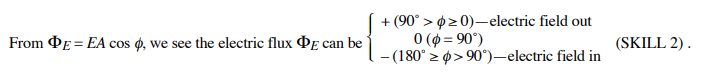
In general, E and/or φ may not be constant over the area, so dΦ_E​ = E cos φ dA, which is the mathematical definition of electric flux:

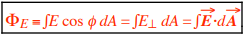
Gauss’s Law Demystified

Alright, we’re about to meet the man himself – Carl Friedrich Gauss, the brain behind Gauss’s Law. Picture this: Gauss was this genius from the 19th century, and he came up with this mind-blowing law that’s the backbone of electromagnetism.

Gauss’s Law, also known as Gauss’s flux theorem, is a fundamental principle in electromagnetism that relates the distribution of electric charge to the resulting electric field. It is one of the four Maxwell equations that form the foundation of electromagnetism. It says that the total electric flux through a closed surface is equal to the total charge enclosed by that surface divided by a constant called the permittivity of free space.

What is Gauss law in simple terms?

Gauss’s law in simpler terms, states the amount of electric field passing through a surface to the charge present inside that surface, providing a mathematical way to understand electric fields around charged objects. to find the non-integral form of Gauss’s law (in vacuum ≈ air):

Where:

• Q_encl is the total charge enclosed within the surface.
• ε_₀ is the permittivity of free space, approximately 8.854×10⁻¹² C²/Nm²

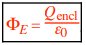
This equation simplifies the process of calculating electric fields for systems with symmetry, as well as the three integral forms of Gauss’s law:

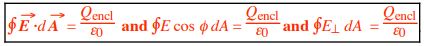
(All forms include “= Q_encl/ε₀ ”.) Recall that ε₀ = 8.854 × 10–12 C²/N·m² . The symbol closed integral symbol means to integrate over a closed surface, so the electric flux Φ_E in Gauss’s law is the net (that is, total) electric flux through that closed surface, and Q_encl is the net (that is, total) charge enclosed by that surface.

Is a Gaussian surface real or imaginary?

A Gaussian surface is a closed mathematical surface whose purpose is to simplify calculations of electric flux. It does not have to coincide with any material surface.

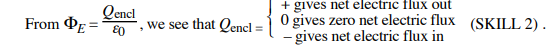
if E = 0 then all excess charge is found on the surface of a solid electrical conductor that has its free charges at rest overall (that is, under electrostatic conditions).

For uniformly distributed charges: the |q| per volume is ρ (rho) (in C/m³),

the |q| per area is σ (sigma) (in C/m²),

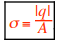
, and the |q| per length is λ (lambda) (in C/m),

where |q| is the absolute value of the charge (in C) spread uniformly over the volume V (in m3), area A (in m²), and/or length L (in m).

Applications of Gauss’s Law

Gauss’s Law is used to calculate the electric field for various charge distributions, especially when the system has symmetry. Here are some key applications:

1. Spherical Charge Distribution: If a sphere has a uniform charge distribution, we can use Gauss’s Law to find the electric field both inside and outside the sphere. Outside the sphere, the electric field behaves as if all the charge were concentrated at the center of the sphere. Inside the sphere, the electric field increases linearly with distance from the center.
2. Cylindrical Charge Distribution: For an infinitely long charged cylinder, Gauss’s Law helps calculate the electric field both inside and outside the cylinder. Inside, the field increases linearly with the radius, while outside it decreases with the square of the distance.
3. Flat Conductor: Gauss’s Law can also be applied to flat conductors to determine the electric field near the surface. For a large conductor with uniform charge distribution, the electric field is constant near the surface and depends on the surface charge density.

Applying Gauss’s law to different shapes

Imagine we have a positively charged sphere, and we want to find the electric field just outside of it. Gauss’s Law to the rescue!

First, we draw a closed surface that encloses the charged sphere. Then, we calculate the total charge enclosed by the surface (remember, the charge inside the bubble!). Once we have that, we divide it by the permittivity of free space and voilà! We’ve got the electric field just outside the charged sphere. Easy-peasy!

What is spherical symmetry in Gauss law?

Spherical symmetry in Gauss’s law refers to a situation where an electric field is radially symmetric around a point charge. The electric flux through a closed spherical surface depends only on the enclosed charge, not its distribution.

1. Finding electric fields from given symmetric charge distributions:
   a) Spherical symmetry: Given a sphere of uniform positive charge density ρ and radius R.
2. Use an integral form of Gauss’s law, for example, o∫ E cos φ dA =Q_encl/ε₀ .
3. Choose a symmetric Gaussian surface: in this case, the surface of a concentric (same center) sphere of radius r.
4. E is away from the enclosed positive charge and so is radially outward while dA is always outwardly normal and so is also radially outward. Therefore, the two vectors E and dA are parallel , so φ = 0 and cos φ = cos 0 = 1 Thus, ∫ E cos φ dA =∫ E (1)dA.
5. E is constant by symmetry, so we can take it out of the integral: ∫ E (1)dA = E ∫ dA.
6. Then∫ dA = A_{spherical surface} = 4πr² so that the left side of Gauss’s law (∫ E cos φ dA) equals E4πr². Therefore,

(telling us that outside of a spherically symmetric charge distribution, the electric field looks like

E =(1/4πε₀)* (|q|/r²) as if all the charge were concentrated at the sphere’s center). For r ≤ R (inside the sphere of charge), there is a charge throughout the entire volume of the Gaussian surface (of radius r). Thus, Q_encl = ρV_encl = ρ4/3πr³, so

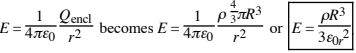
What is the Gauss law for flat symmetry?

Flat symmetry: Given a very large flat horizontal conductor with its free charges at rest overall. It has a
uniform negative surface charge density –σ on its bottom surface and no other excess charge.

1. Use an integral form of Gauss’s law, for example, ∫ E cos φ dA =Q_encl/ε₀ .
2. Choose a symmetric Gaussian surface: in this case, the surface of a cylinder with its vertical axis perpendicular to the bottom surface of the conductor. The top and part of the side of the Gaussian cylinder are in the material of the conductor. The bottom of the Gaussian cylinder is below the flat conductor’s bottom surface and has area A.
3. Break the integral into three parts: ∫ E cos φ dA = ∫E cos φ dA (top) +∫E cos φ dA (side)+ ∫E cos φ dA (bottom).
4. In the material of a conductor with free charges at rest overall, E = 0, so ∫E cos φ dA = ∫0 cos φ dA = 0. (That is, there is no electric flux ΦE through the top.)
5. Part of the side is in the conductor where E = 0. The rest of the side is outside the conductor where E is toward the enclosed – charge, making E parallel to the side. dA is always outwardly normal and so is perpendicular to the side. Therefore, the two vectors E and dA are perpendicular to one another , so cos φ = cos 90 ̊ = 0 so ∫E cos φ dA = ∫0 dA = 0. (That is, there is no electric flux ΦE through the side.)
6. Over the bottom of the Gaussian surface: E is toward the enclosed – charge and so is toward the bottom surface of the conductor. dA is always outwardly normal and so is away from the bottom surface of the conductor. Therefore, the two vectors E and dA are antiparallel (opposite) to one another , so φ = 180 ̊ and cos φ = cos 180 ̊ = –1. Thus, ∫E cos φ dA = ∫E(–1)dA .
7. E is constant by symmetry, so we can take it out of the integral: ∫E(–1)dA = –E ∫dA .
8. Then ∫dA = A. Thus, the left side of Gauss’s law (o∫ E cos φ dA ) equals 0 + 0 + (–EA) = –EA.
9. Since Q_encl = –σA, o∫ E cos φ dA =Q_encl ε₀ becomes –EA = –σAε0 , or E = σ/ε₀

What is the Gauss law for cylindrical symmetry?

The Gauss law for cylindrical symmetry states that the electric flux through a closed cylindrical surface is proportional to the total charge enclosed within the cylinder. Cylindrical symmetry: Given a very long rod of charge of radius R, much larger length L, volume charge density ρ, and linear charge density λ.

1. Use an integral form of Gauss’s law, for example, o∫ E cos φ dA =Q_encl/ε₀ .
2. Choose a symmetric Gaussian surface: in this case, the surface of a coaxial (same axis) cylinder of radius r and length l (l << L).
3. Break the integral into three parts: o∫ E cos φ dA = ∫E cos φ dA + ∫E cos φ dA + ∫E cos φ dA.
4. Over both ends: E→ is away from the enclosed + charge and so is radially outward. dA→ is always outwardly normal and so is parallel to the axis of the coaxial cylinder. Therefore, the two vectors E→ and dA→ are perpendicular, so φ = 90 ̊ and cos φ = cos 90 ̊ = 0. Thus, ∫E cos φ dA = 0 =∫E cos φ dA . (That is, there is no electric flux Φ_E through the ends.)
5. Over the side: E is away from the enclosed + charge and so is radially outward. dA is always outwardly normal and so is also radially outward. Therefore, the two vectors E and dA are parallel, so φ = 0 and cos φ = cos 0 = 1. Thus, ∫E cos φ dA = ∫E(1)dA .
6. E is constant by symmetry, so we can take it out of the integral: ∫E(1)dA = E ∫side dA .
7. Then ∫dA = A_side = 2πrl. Thus, the left side of Gauss’s law (∫ E cos φ dA ) equals 0 + E2πrl + 0 = E2πrl.
8. For r ≥ R (outside the cylindrical charge distribution), Q_encl = ρπR²l or λl.
9. Thus, ∫ E cos φ dA = Q_encl/ε₀ becomes E2πrl =ρπR²l or λl/ε₀ . Solving,

Understanding Electric Fields and Their Behavior

Before we go further, let’s talk about electric fields – those invisible forces that interact with charged particles like they’re having a secret dance party. You’ve probably experienced electric fields firsthand when you got zapped by static electricity, right?

These fields surround charged particles like a protective bubble and can either attract or repel other charged particles. They’re like the puppeteers pulling the strings of charged objects, making them dance to their electrifying tune.

How Electrical Flux and Gauss’s Law Shape Electric Fields

Now, let’s see how electrical flux and Gauss’s Law come together to shape electric fields. Imagine you have a closed surface (like a magical bubble) surrounding a charged object. Gauss’s Law tells us that the total electric flux passing through that surface is directly related to the total charge enclosed by the bubble.

When we know the charge inside the bubble and the shape of the bubble’s surface, we can use Gauss’s Law to calculate the electric field at any point outside the charged object. It’s like peeking inside the bubble and knowing exactly what’s going on with the electric field outside.

Finding a charge distribution from a known electric field:

Using Gauss’s Law, we can also deduce the charge distribution if the electric field is known. In conductors, the electric field inside the conductor is zero under electrostatic conditions. This is because any free charges within the conductor will move until the electric field inside cancels out.

For example, consider a conductor with a cavity containing a charge q. According to Gauss’s Law, the charge on the inner surface of the cavity is equal in magnitude but opposite in sign to the charge inside the cavity. Any excess charge resides on the outer surface of the conductor.

Real-World Applications and Implications

Now, you might wonder, “Why do we even bother with all this electric field stuff?” Well, my friends, understanding electrical flux and Gauss’s Law is crucial in designing and building all the cool electronic gadgets we love!

Think about it – from your smartphone to your computer, everything runs on electricity. And to make these devices work efficiently and safely, engineers need to know how electric fields behave in different situations.

For example, when it comes to transmitting power over long distances, knowing how electrical flux distributes can help us design more efficient power lines. It’s like having a superpower to optimize energy transmission!

But wait, there’s more! Ever heard of electromagnetic compatibility testing? It’s like a compatibility check for electronic devices, making sure they play nice with each other without causing interference. Understanding electrical flux and Gauss’s Law plays a key role in this too!

So, my friends, the world of electrical flux and Gauss’s Law might seem like a complex web of equations and theories, but it’s what makes our modern technology dance to the tune of electricity. Embrace the knowledge, and who knows, you might be the next genius engineer shaping the future of electromagnetic wonders!

And hey, let’s not forget about electromagnetic shielding – the superhero of electronic protection. We use this concept to create shields that keep unwanted electromagnetic fields from messing with our sensitive electronic equipment. Gauss’s Law helps us understand how to set up these shields and keep our gadgets safe and sound.

Now, I know we’ve covered a lot, and you might be thinking, “Do I really need to know all this to get through life?” Well, maybe not for everyday tasks, but having a basic understanding of electrical flux and Gauss’s Law can be super handy. Next time you use your smartphone, watch a movie on your tablet, or turn on a light switch, just remember that all of that tech magic is happening thanks to these fundamental principles.

Key Takeaways

• Electric flux is a measure of the electric field passing through a surface and is calculated as the dot product of the electric field and the area vector.
• Gauss’s Law relates electric flux to the enclosed charge, providing a powerful tool for calculating electric fields in systems with symmetry.
• Applications of Gauss’s Law include spherical, cylindrical, and flat charge distributions, each with unique electric field behavior.
• Conductors and Cavities: Inside a conductor, the electric field is zero, and charge resides on the surface. If there is a cavity inside the conductor, any charge placed inside induces an equal but opposite charge on the cavity’s inner surface.

These concepts form the foundation for understanding electromagnetism and are essential for solving problems involving electric fields and charge distributions in various physical systems.

Class notes