Understanding Ray Optics

Ray optics, also known as geometrical optics, is a fundamental area of physics that describes the behavior of light in terms of rays. A ray is essentially an imaginary line that represents the path along which waves travel. This field provides insight into how light interacts with various surfaces and materials.

Wave Fronts and Rays

In optics, a ray is a simplified geometric representation of light or other electromagnetic radiation. It is defined as a curve that is perpendicular to the wavefronts of the light and indicates the direction in which energy propagates. In a medium that is uniform in composition (homogeneous) and exhibits identical optical properties in all directions (isotropic), these rays remain straight and are always perpendicular to the wave fronts.

What are waves fronts?

A wavefront is an imaginary surface that connects points on a wave that oscillate in sync. It represents all locations in a medium where the wave maintains the same phase, whether at the crests, troughs, or any intermediate stage of the wave cycle.

What does reflection mean in science?

Reflection is the sudden change in the direction of a wave when it encounters the boundary between two different media. A portion of the incoming wave remains within the original medium, continuing to propagate.

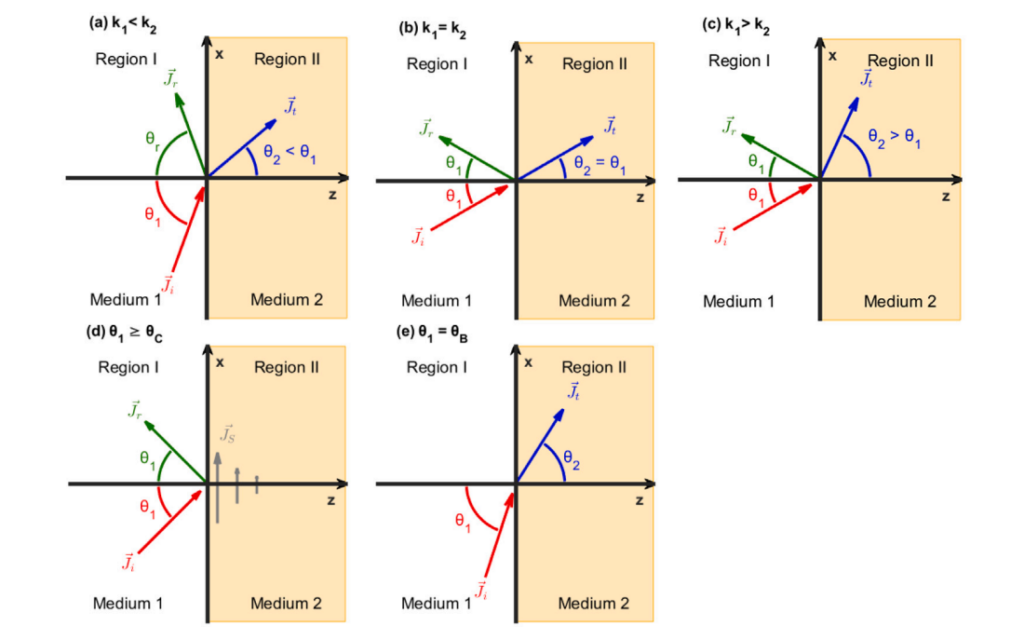
Reflection occurs when a light wave bounces off a surface. The law of reflection states that the angle of incidence (θₐ) is equal to the angle of reflection (θᵣ), and both lie in the same plane.

Refraction and Snell’s Law

Snell’s law, also called the law of refraction, explains how waves, including light, alter their direction when crossing the interface between two distinct isotropic media. Snell’s law is based on Fermat’s principle of least time, which asserts that light travels between two points along the path that requires the shortest time.

Refraction occurs when a wave passes from one medium (medium A) into another (medium B) across a boundary (Since a is the first letter of our alphabet Medium A is designated as the initial medium where the light originates). The angle of refraction (θ_b) depends on the indices of refraction (n) of the two media. The refracted ray is in the same plane as the incident ray, the reflected ray, and their normal.

The index of refraction

The index of refraction, also known as the refractive index (n), is a fundamental property of optical materials. The index of refraction is a dimensionless value that represents the degree to which light bends or changes direction when passing into a material. So, for the manufacturing of any optical device, the calculation of “n” is considered very important. The index of refraction, n, is defined by the equation n=c/υ, where:

• c is the speed of light in a vacuum, precisely 299,792,458299,792,458 m/s (approximately 2.998×10⁸ m/s).
• υ represents the speed of light in a given medium, which is always less than or equal to c (υ≤c).

Since the index of refraction is a ratio of speeds, it is a dimensionless quantity. It is always greater than or equal to 1 (n≥1), with n = 1 in a vacuum and n ≈ 1 in air.

What is the Snell’s law?

Snell’s law of refraction states that for a given pair of media, the ratio of the sine of the angle of incidence to the sine of the angle of refraction remains constant. Snell’s Law governs this phenomenon: n_asin⁡θ_a=n_bsin⁡_θb

where:

• nₐ and n_b are the indices of refraction of the respective media.
• θₐ and θ_b are the angles of incidence and refraction, respectively.

When light moves into a medium with a higher refractive index (n), it bends toward the normal. Conversely, when moving to a lower n, it bends away from the normal.

When a wave refracts across a boundary, neither wave generation nor absorption occurs, meaning the frequency (f) remains unchanged. In a vacuum, the relationship is given by c=λ₀f, while in a medium with refractive index n, the speed of light is υ=c/n, leading to υ=λf. Eliminating f from these equations gives: λ=λ₀ /n

where λ₀ is the wavelength in a vacuum and λ is the wavelength in the medium. Since n≥1, it follows that λ≤λ₀, meaning the wavelength shortens as light enters a medium with a higher refractive index.

Total Internal Reflection

When light travels from a medium with a higher n to one with a lower n, it may undergo total internal reflection if the angle of incidence exceeds the critical angle (θ_crit). The critical angle is found using: sin⁡θ_crit=n_b/n_a

For angles greater than θ_crit, all the incident light reflects back into the original medium. This principle is used in fiber optics and other applications.

What is the dispersion of light?

Dispersion occurs when different wavelengths of light refract at different angles, causing the separation of white light into a spectrum. This wavelength-dependent variation in the index of refraction is responsible for effects like rainbows and the splitting of light through prisms. The colors in the spectrum of light are Violet, Indigo, Blue, Green, Yellow, Orange and Red.

Polarization of Light

Unpolarized light or natural light consists of waves vibrating in multiple directions. When light passes through a polarizer, only the components oscillating parallel to the polarizing axis are transmitted. A second polarizer, known as an analyzer, can further filter the light. The intensity of transmitted light through the analyzer follows Malus’ Law: I=I_max⁡cos⁡²φ

where:

• I_max is the maximum transmitted intensity (in W/m²). of the light after passing through the ideal polarizer: I_max =0.5I_o if the original incident light (of intensity I_o) is “unpolarized”.
• I is the intensity (in W/m²) of the light after passing through the ideal analyzer
• φ is the angle between the axes of the polarizer and analyzer.

Light reflected at a specific angle, known as Brewster’s angle (θ_p), becomes completely polarized. This angle satisfies: tan⁡θ_p=n_b/n_a

What is the Huygens principle in simple words?

Huygens’ Principle asserts that each point on a wavefront serves as a source of secondary spherical wavelets, with the new wavefront at any later time forming as the envelope of these wavelets. The new wave front is the envelope of these wavelets at a later time. This principle helps derive the laws of reflection and refraction.

By decomposing complex wavefronts into simpler secondary sources, this principle provides a clear framework for understanding wave behavior. It plays a crucial role in wave optics and has widespread applications in physics and engineering.

Conclusion

Ray optics provides a fundamental framework for analyzing the behavior of light as it interacts with different surfaces and materials. By treating light as rays that follow geometric principles, we can explain key phenomena such as reflection, refraction, dispersion, and total internal reflection. Laws like Snell’s law and the reflection principle help us predict how light bends and reflects at interfaces, establishing the basis for technologies such as lenses, mirrors, fiber optics, and optical instruments.

While ray optics simplifies the complex nature of light by ignoring its wave characteristics, it remains an essential tool for engineering and scientific applications. Understanding these principles not only enhances our grasp of optical systems but also bridges the gap to more advanced topics like wave optics and quantum optics. As optical technologies continue to evolve, the principles of ray optics will remain a cornerstone of innovation in fields ranging from telecommunications to medical imaging.