Thermodynamics: Entropy and the Second Law

Thermodynamics is a fundamental physics and engineering branch governing energy transfer and transformation. Among its key principles, the Second Law of Thermodynamics plays a crucial role in defining the direction of processes, the concept of entropy, and the efficiency of thermal systems. This article explores key thermodynamic principles, including reversible and irreversible processes, entropy, and isentropic efficiencies.

What is a reversible and irreversible process in thermodynamics?

In thermodynamics, reversible processes are those that can occur in both directions (1 → 2 and 2 → 1) spontaneously, without requiring additional energy input from the surroundings. A reversible process is an idealized process that can be reversed without leaving any trace on the system or surroundings. It occurs infinitely slowly and involves no dissipative effects such as friction, unrestrained expansion, or mixing.

In reality, however, all processes are irreversible, meaning they involve some degree of entropy generation. Irreversible processes proceed in only one direction and cannot be reversed without an external energy input. Irreversibilities determine the direction of a thermodynamic process. We try to minimize factors causing irreversibility to optimize performance.

In real-world applications, several factors contribute to irreversibilities, such as finite temperature differences, friction, chemical potential differences, dissipative effects, sudden expansion, hysteresis, and the nonelastic expansion of materials.

Second Law of Thermodynamics Statements

The Second Law can be expressed in multiple ways, with two widely accepted statements:

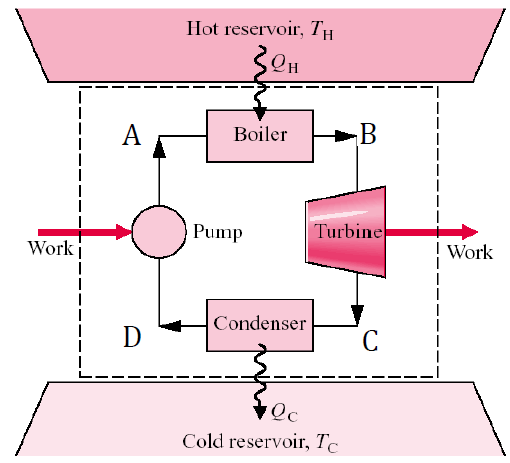
1. Kelvin-Planck Statement – It is impossible to construct a heat engine that operates in a thermodynamic cycle and produces power while exchanging heat with only a single thermal reservoir. In other words, heat engines must interact with two thermal reservoirs—a heat source and a heat sink. As a result, not all heat supplied to a heat engine can be converted into useful work; a portion of the thermal energy must be transferred to the heat sink.
2. Clausius Statement – Heat cannot spontaneously transfer from a lower-temperature source to a higher-temperature medium without an external energy input. In other words, transferring heat from a cooler medium to a warmer one requires a heat pump, which consumes external energy, typically in the form of mechanical power. While heat naturally flows from high-temperature to low-temperature regions, the reverse process does not occur without assistance, making heat transfer an inherently irreversible process.

The Kelvin-Planck statement applies to heat engines, while the Clausius statement pertains to refrigerators and heat pumps. These two principles are equivalent, as violating one would inherently lead to the violation of the other, and vice versa.

Second Law Corollaries

From these statements, several corollaries arise:

• No heat engine can be more efficient than a Carnot engine operating between two temperature reservoirs.
• Any reversible heat engine operating between two reservoirs is as efficient as any other one operating between the same reservoirs.
• The coefficient of performance (COP) of a reversible refrigerator or heat pump is always greater than that of an irreversible one operating between the same reservoirs.

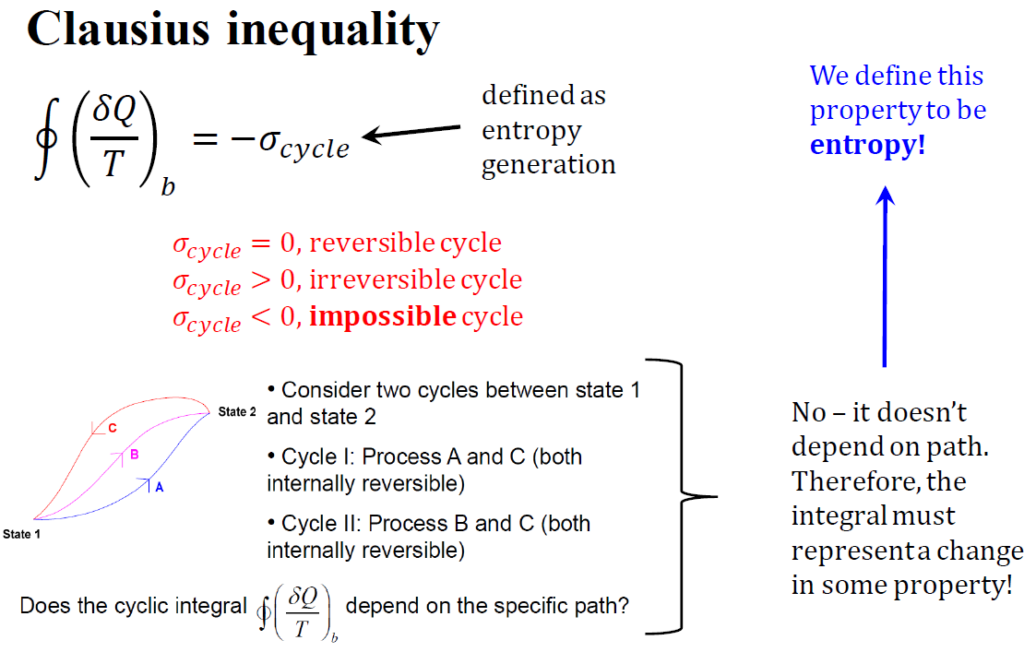
What is meant by Clausius’s inequality?

The Clausius inequality arises from applying the second law of thermodynamics to each infinitesimal heat transfer stage. It is a fundamental expression of the second law, formulated by German physicist R.J.E. Clausius. This inequality provides a crucial mathematical framework for understanding entropy and the behavior of thermodynamic systems. According to Clausius’s statement, creating a device whose only effect is transferring heat from a cooler reservoir to a hotter one is impossible.

What is entropy in simple terms?

Entropy (S) measures disorder or randomness in a system. The higher the entropy, the more chaotic and less organized the system becomes.

In thermodynamics, entropy describes how energy spreads within a system. It reflects the degree of microscopic disorder, where energy naturally tends to disperse rather than remain concentrated. This concept helps explain why certain processes, like heat flowing from hot to cold objects, happen spontaneously. The entropy change of a system is given by:

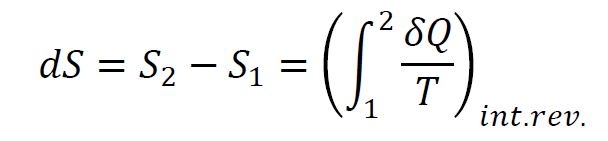
How is entropy measured?

Entropy is measured in joules per kelvin (J/K) as it represents the amount of energy dispersed per unit temperature. It is an extensive property, meaning it depends on the size or mass of the system.

For a more specific measurement, specific entropy (𝑠) is used, which is entropy per unit mass and has units of J/(kg·K).

In practical applications, entropy values for real substances are often determined using thermodynamic property tables, similar to other thermodynamic properties like enthalpy and internal energy.

What is an example of entropy in everyday life?

An example of entropy in everyday life is boiling water. As water is heated, its molecules move more rapidly, becoming more disordered, which increases the system’s entropy. Other common examples include:

• Breaking an egg – The structured form of the egg is disrupted, increasing disorder.
• Mixing sugar in coffee – The sugar dissolves and spreads, leading to a more disordered state.
• Smelling perfume – Perfume molecules disperse from a concentrated state to fill the room, increasing entropy.
• Rubbing hands together – The heat generated by friction increases the system’s entropy.

Each of these examples demonstrates how energy disperses and disorder naturally increases in a system. Beyond thermodynamics, entropy is also used in fields like information theory and ecology to describe uncertainty, randomness, or the distribution of resources.

T-ds Relations

The T-ds equations are derived from the First and Second Laws of Thermodynamics. 𝑇−𝑑𝑆 relations are a way to obtain specific entropy from other properties. 𝑇−𝑑𝑆relations are:

Tds=du+Pdv

Tds=dh−vdP

where du and dh represent changes in internal energy and enthalpy, respectively. These relations are crucial for analyzing thermodynamic cycles.

Ideal Gas Entropy Lookups

For ideal gases, entropy is a function of temperature and pressure (or volume). Using thermodynamic tables, entropy values can be looked up for different states. Alternatively, entropy changes can be computed using:

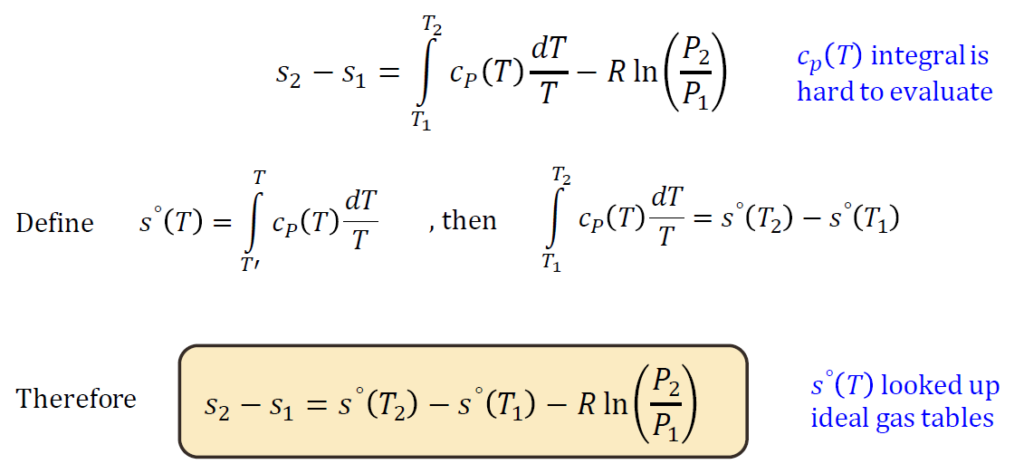
where R is the specific gas constant, and cp, cv specific heats. note: 𝑐_𝑝(𝑇) integral is
hard to evaluate

How can entropy change be evaluated?

Depending on the system and available data, entropy change can be evaluated using various methods. One approach is the products minus reactants rule, where the total entropy of reactants is subtracted from the total entropy of products in a chemical reaction. Another method involves using heat capacity measurements along with enthalpy values for fusion or vaporization, particularly for phase transitions. For real substances like water, entropy values are typically looked up in thermodynamic property tables, similar to other properties such as internal energy, enthalpy, and volume. In the case of incompressible substances like solids and liquids, entropy change is often determined using specific heat capacity data.

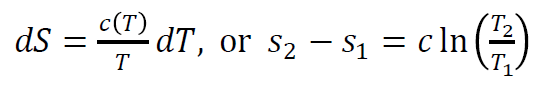
For ideal gases, entropy is a function of both temperature and pressure and can be calculated using the equation:

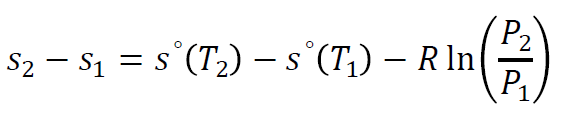
where tabulated values for s∘(T) are used from ideal gas property tables.

What is the general entropy balance equation?

The general entropy balance equation expresses that in any isolated system, entropy always increases due to spontaneous processes, as entropy is not conserved like mass or energy. Instead, it is generated within the system due to process irreversibilities. This means that the entropy leaving a control volume is always greater than the entropy entering it, accounting for the entropy generation caused by irreversibilities. The entropy balance equation is typically written as:

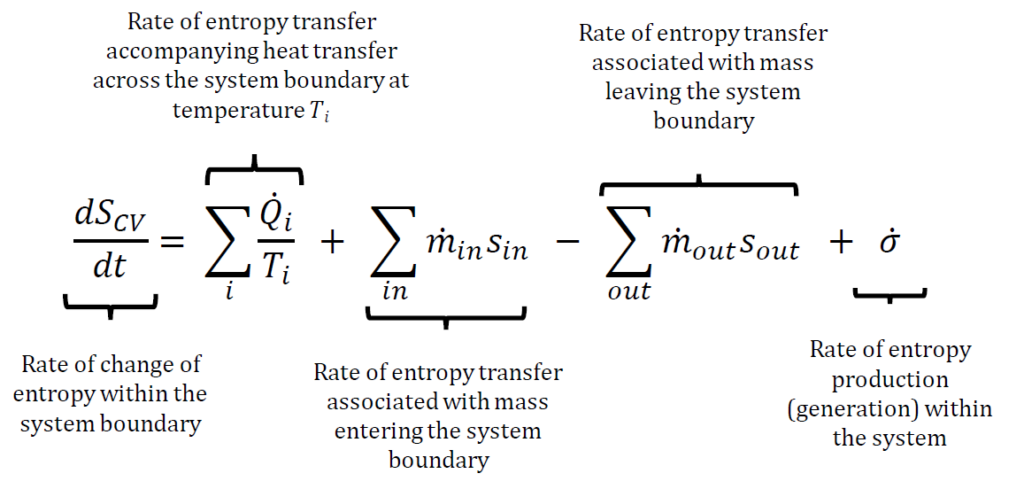
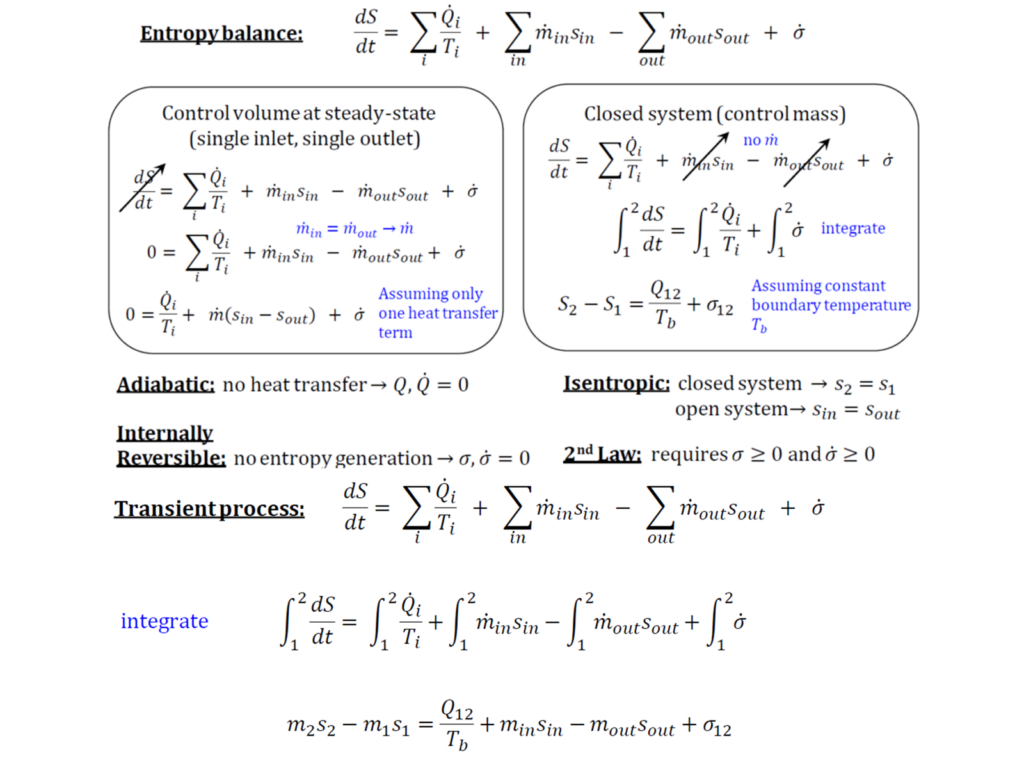
Does isentropic mean no change in entropy?

An isentropic process is one in which the system’s entropy remains constant, meaning there is no change in entropy (Δs= 0). These processes are adiabatic, with no heat transfer into or out of the system, and are also reversible, assuming no friction or dissipative effects. Because of this, isentropic processes are highly thermodynamically efficient and are commonly used in idealized models of gas turbines and compressors.

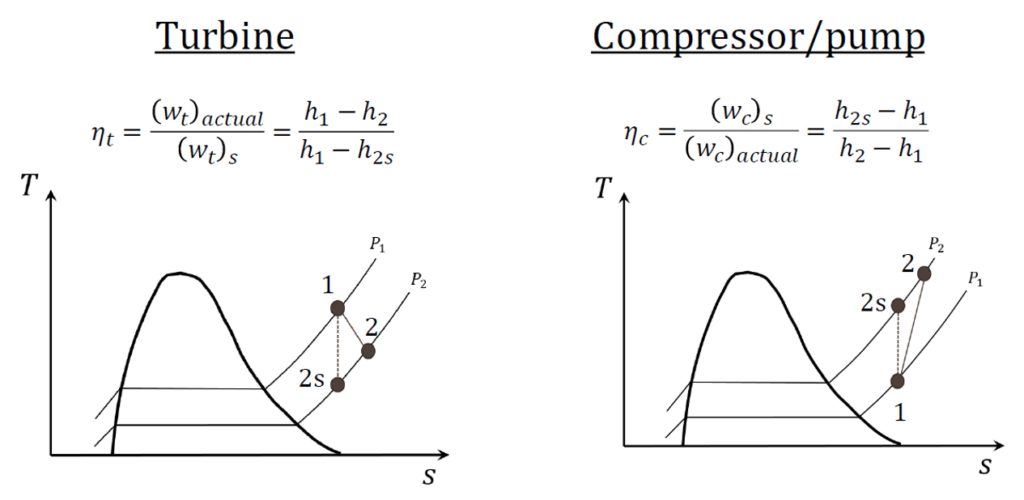
What is the isentropic efficiency of steady-flow devices?

The isentropic efficiency of steady-flow devices, such as turbines, compressors, and nozzles, measures how closely the device’s actual performance approaches the ideal isentropic process. For a turbine, it is defined as the ratio of the actual work output to the work output in an ideal isentropic process, assuming no entropy change. This efficiency helps quantify the energy degradation in real systems due to irreversibilities such as friction and heat losses.

Engineers use isentropic efficiency to compare the real performance of a device to its idealized counterpart under the same inlet and exit conditions, where the entropy at the isentropic exit state (s_2s=s₁​) and the exit pressure (P_2s=P₂ ) is maintained. A high-efficiency value indicates minimal energy losses due to irreversibilities.

• Turbine efficiency: η_turbine=Actual work output/ Isentropic work output
• Compressor efficiency η_compressor=Isentropic work input/Actual work input
• Nozzle efficiency: η_nozzle=Actual kinetic energy increase/Isentropic kinetic energy increase

Conclusion

In conclusion, entropy and the second law of thermodynamics play a fundamental role in understanding the behavior of energy in physical systems. Entropy serves as a measure of disorder and irreversibility, dictating the natural direction of thermodynamic processes. The second law establishes that energy transformations are inherently inefficient, with some energy inevitably dissipating as unusable heat. These principles are essential in engineering applications, from power generation to refrigeration, influencing the design and efficiency of real-world systems.

By understanding entropy and the second law, scientists and engineers can develop innovative solutions to optimize energy use and minimize losses, ultimately improving technological advancements and sustainability efforts.