Thermodynamics Crashcourse: Principles and Closed System
Thermodynamics is a fundamental branch of physics and engineering that governs how energy is transferred, converted, and conserved in a system. From engines and refrigerators to power plants and climate systems, thermodynamic principles are crucial in understanding and optimizing energy use.
In this crash course, we will explore the core principles of thermodynamics, focusing on closed systems, which allow energy exchange but prevent mass transfer. This article provides a concise yet comprehensive overview of thermodynamic fundamentals by breaking down key concepts such as the laws of thermodynamics, energy conservation, heat transfer, and work interactions. Whether you’re a student, engineer, or simply curious about how energy behaves, this guide will help you grasp the essential principles that drive countless real-world applications.
The Laws of Thermodynamics
Thermodynamics is the science of energy and exergy, founded on fundamental principles. The term “energy” conveys the concept of the ability to cause change. The word “thermodynamics” originates from the Greek words therme (meaning heat or thermal energy) and dunamis (meaning power). This origin aptly describes many modern energy production processes, where thermal energy is converted into work or electrical energy. Thermodynamics’ study and analytical methods are based on three fundamental laws: the zeroth, first, and second laws. These laws are named according to their numerical order rather than the chronological sequence in which they were discovered.
- The Zeroth Law establishes the concept of thermal equilibrium, meaning if two bodies are each in equilibrium with a third, they must be in equilibrium with each other. This sets the foundation for temperature measurement.
- The First Law of Thermodynamics, also known as the energy conservation principle, states that energy cannot be created or destroyed; that while energy can be transformed between different forms, the total energy of a closed system remains constant, essentially, “the best you can do is tie” by perfectly conserving energy.
- The Second Law of Thermodynamics dictates that entropy, or disorder, always increases in real processes, making it impossible to achieve a perfect conversion of energy into useful work, meaning “you can never tie” because every energy transformation leads to some unavoidable losses.
Together, these principles define the limits of energy interactions in the universe.
Closed System
A thermodynamic system is classified as a closed energy system when it exchanges energy with its surroundings solely in the forms of thermal energy and work while its mass remains constant (i.e., no mass enters or leaves the system). Due to this characteristic, closed systems are often referred to as fixed-mass systems. Any system meeting these conditions is considered a closed energy system.
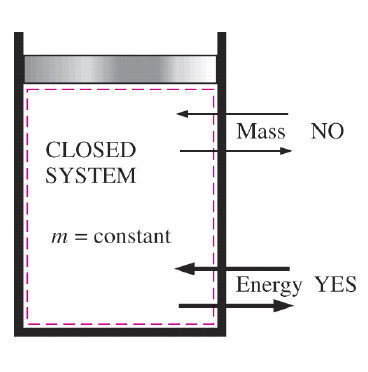
For instance, the pizza shown below does not qualify as a closed energy system because, as it cools, it loses mass to the surroundings in the form of moisture (H₂O). The energy and exergy analyses of such systems are explored in detail in the following section, using the examples of a rigid tank system and a piston-cylinder system.

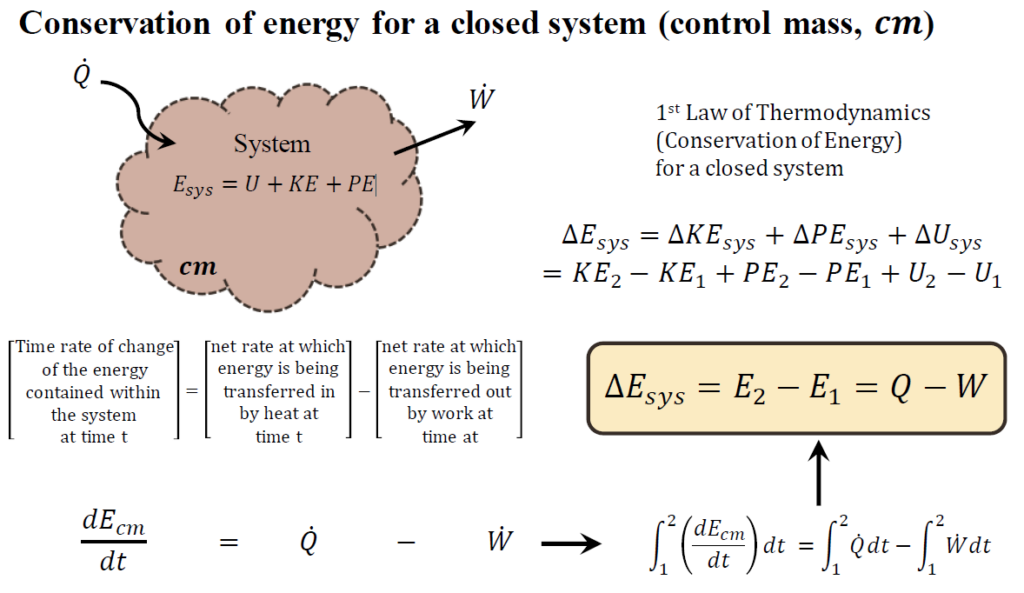
Conservation of energy for a closed system (control mass)
The Conservation of Energy for a Closed System (Control Mass) states that the total energy within a system changes based on the net heat added and the work done by or on the system. Mathematically, this is expressed as: dEcm/dt=Q_dot−W_dot
This equation describes the time rate of change of the energy contained within the system at time t. It is determined by:
- The net rate at which energy is transferred into the system by heat (Q).
- The net rate at which energy is transferred from the system by work (W).
For a finite change between two states (initial and final), this simplifies to: ΔEsys=E2−E1=Q−W
where:
- E2 and E1 are the system’s total energy at the final and initial states.
- Q represents the heat added to the system.
- W represents the work done by the system on its surroundings.
This equation directly applies the First Law of Thermodynamics, ensuring that energy is neither created nor destroyed but only transferred between heat, work, and stored internal energy within the system.
What is the relationship between heat and work in thermodynamics?
The relationship between heat and work in thermodynamics is fundamental and governed by the laws of thermodynamics. The fundamental principle states that the change in energy of a closed system is equivalent to the heat added to the system plus the work done on the system. This total energy is typically represented by internal energy (U), expressed mathematically as ΔU=Q+W. In flow systems, we introduce enthalpy (H), whose change also follows the same relationship: ΔH=Q+W.
Mechanical forms of work
Mechanical work can take various forms depending on how energy is transferred within a system.
- Acceleration work, associated with kinetic energy, occurs when a force accelerates a body, increasing its velocity.
- Work to raise a body in a potential field, commonly known as potential energy, is performed when lifting an object against gravitational or other force fields.
- Spring work involves the compression or extension of a spring, storing energy in its deformation.
- Shaft work is transmitted through rotating elements such as gears or turbines, commonly found in mechanical power systems.
- Electrical work results from the movement of electric charges, often seen in motors and electrical circuits.
Each of these work forms represents a method of energy transfer, playing a crucial role in thermodynamic and mechanical systems.
Characteristics of work
Work in thermodynamics is defined as energy transfer between a system and its surroundings, occurring when the sole effect on the external environment could have been the raising of a weight. Several key characteristics define work:
- Crosses the system boundary, meaning it either enters or leaves the system. Unlike energy or properties such as temperature and pressure
- Work is not a property of a system but rather a quantity associated with a process, meaning it depends on the change of states.
- Additionally, work is path-dependent, meaning its value varies based on how the process occurs rather than just the initial and final states.
The sign convention for work states that work is positive (W>0) when the system does work on its surroundings (work output) and negative (W < 0) when work is done on the system (work input). These principles are fundamental in analyzing energy transfer in thermodynamic systems.
Moving boundary work
Moving boundary work occurs when a system undergoes expansion or contraction, causing its boundary to move. This type of work is particularly relevant in systems where the volume of fluid changes, such as in piston-cylinder arrangements inside an internal combustion engine. The work done by or on the system is given by the following equation W=∫VPdV.
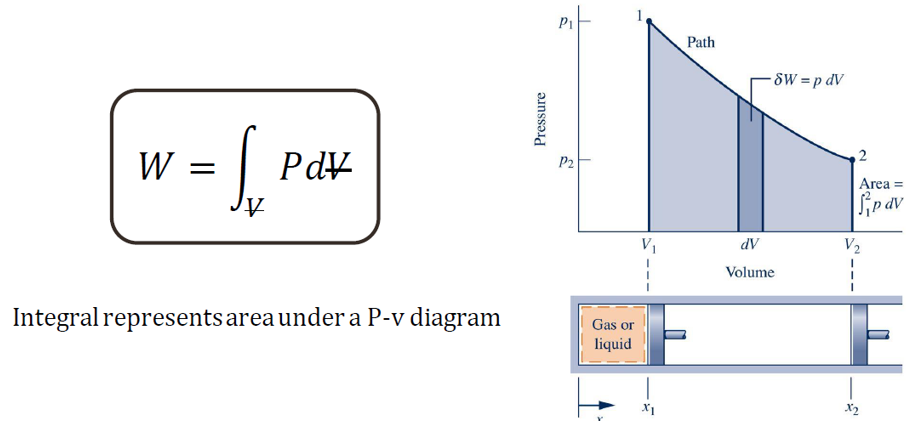
Where pressure P acts on the system boundary as the volume V changes. This interaction between the system and its surroundings results in energy transfer, playing a key role in thermodynamic processes such as compression and expansion in engines and refrigeration cycles.
What is the polytropic process law?
The polytropic process equation is derived from the ideal gas law PV=mRT, where m represents the mass of the gas, R is the specific gas constant, and T denotes the temperature. However, additional factors must be considered, as the polytropic equation accounts for heat capacity ratios and the molecular properties of the gas.
A polytropic process is a thermodynamic process in which pressure and volume follow the relationship PVn = constant, where n is the polytropic coefficient. This coefficient determines the nature of the process and can take different values depending on the specific thermodynamic conditions. Polytropic processes are widely used to describe real gas behavior in compression and expansion, as they generalize various thermodynamic processes, including isothermal (n = 1), adiabatic (n = γ), and isentropic processes.

Heat Transfer Summary
Heat transfer is the energy exchange between a system and its surroundings that occurs without mass transfer or work. This transfer is driven by a temperature difference, where heat naturally flows from a higher-temperature region to a lower-temperature region. Similar to work, heat is a path function, meaning its value depends on the process rather than the initial and final states of the system. Heat transfer follows a sign convention: when heat enters the system (Q>0), it is considered heat input, while when heat leaves the system (Q < 0), it is considered heat output. Understanding heat transfer is essential in thermodynamics, as it plays a crucial role in energy exchange processes such as heating, cooling, and phase changes.
Heat transfer follows a sign convention: when heat enters the system (Q>0), it is considered heat input, while when heat leaves the system (Q < 0), it is considered heat output. Understanding heat transfer is essential in thermodynamics, as it plays a crucial role in energy exchange processes such as heating, cooling, and phase changes.
Heat Transfer Modes
- Conduction: Transfer due to temperature difference within a solid or stationary fluid.
- Convection: Transfer between a solid and a moving fluid.
- Radiation: Emission of electromagnetic waves from a surface.
Summary of phases
In thermodynamics, substances can exist in different phases, which are classified based on their position relative to the vapor dome on a phase diagram. A compressed liquid exists to the left of the vapor dome, meaning it is below its boiling point at a given pressure. A saturated liquid is located on the vapor dome but to the left of the critical point, meaning it is at its boiling temperature and ready to transition into vapor.

A saturated liquid-vapor mixture lies under the vapor dome, representing a two-phase region where pressure and temperature are dependent properties, requiring an additional property to define the state. A saturated vapor is found on the vapor dome, to the right of the critical point, meaning it is at the edge of condensation. Moving further right, superheated vapor exists beyond the vapor dome, where the substance is in a gas phase above its boiling point at a given pressure. Understanding these phase classifications is essential in analyzing thermodynamic cycles and phase-change processes.
What is the critical point in thermodynamics?
The critical point is the temperature and pressure at which saturated liquid and saturated vapor become indistinguishable, beyond which distinct liquid and vapor phases do not exist.
What are saturation temperature and saturation pressure in thermodynamics?
The saturation temperature is the temperature at which phase change occurs for a given pressure, while the saturation pressure is the pressure at which phase change occurs for a given temperature.
Thermodynamic Property Evaluation
In thermodynamics, property evaluation is essential for defining the state of a substance and determining its characteristics. For simple compressible substances, a state is fully defined by any two independent, intensive properties, allowing all other properties at that state to be determined.
Thermodynamic properties are commonly organized in tables, which provide data for different phases, including compressed (subcooled) liquid, saturated liquid, liquid-vapor mixtures, saturated vapor, and superheated vapor. These tables list specific properties, which are values per unit mass, including specific volume (𝑣 = V/m), specific internal energy (𝑢= U/m), specific enthalpy (ℎ= H/m), and specific entropy (𝑠= S/m).
Understanding these properties and how to retrieve them from tables is crucial for analyzing thermodynamic systems, especially in energy conversion and phase-change processes.
How do you determine the thermodynamic properties of a substance?
Property determination in thermodynamics follows a systematic approach to define the state of a substance. First, it is essential to identify two independent intensive properties that are available, following the state principle. Next, the phase of the substance must be determined, classifying it as compressed liquid (CL), saturated liquid (Sat. L), saturated liquid-vapor mixture (SLVM), or saturated vapor (Sat. V).

Once the phase is identified, the appropriate property table is selected to retrieve the necessary data. If compressed liquid data is unavailable, a suitable approximation can be used to estimate the properties. This structured process ensures accurate evaluation of thermodynamic properties, which is critical for analyzing energy and phase-change systems.
What is quality in thermodynamics?
Quality (x) is an intensive thermodynamic property that defines the proportion of vapor in a saturated liquid-vapor mixture (SLVM). It is calculated as the mass of vapor divided by the total mass of the mixture, with values ranging between 0 (saturated liquid) and 1 (saturated vapor).
Quality is only relevant inside the vapor dome and does not apply to compressed liquid or superheated vapor states. At any point within the vapor dome, key thermodynamic properties can be determined using quality: specific volume (v= vf + x (vg – vf)), specific internal energy (u= uf +x (ug– uf)), specific enthalpy (h = hf + x (hg – hf)), and specific entropy (s = sf + x (sg – sf)). These relationships allow for the precise calculation of properties in two-phase systems, which is essential for analyzing phase-change processes in thermodynamics.
CL tables
Compressed Liquid (CL) Tables are structured based on pressure and corresponding saturation temperature, providing thermodynamic properties at various temperatures for a given pressure. When compressed liquid data is unavailable, approximations can be used as a last resort. Since liquids are generally incompressible, meaning changes in pressure (ΔP) have minimal effects on specific volume (v) and internal energy (u), their properties can be estimated using saturated liquid values.
Under this assumption, approximations include:
- 𝑢≈𝑢𝑓𝑇
- 𝑣≈𝑣𝑓𝑇
- ℎ≈𝑢𝑓𝑇+𝑃𝑣𝑓𝑇≈ℎ𝑓𝑇+𝑣𝑓𝑇[𝑃−𝑃𝑠𝑎𝑡𝑇]
These estimations are useful when compressed liquid tables are unavailable, allowing for reasonable property calculations in thermodynamic analyses.
What is the T-v diagram in thermodynamics?
A T-v diagram (temperature-specific volume plot) in thermodynamics is a graphical representation that illustrates the relationship between temperature (T) and the specific volume (v) of a substance. In this diagram, temperature is plotted on the y-axis, while specific volume is on the x-axis, allowing for a clear visualization of phase changes, such as the transition from liquid to vapor.

The T-v diagram is particularly useful for analyzing processes involving temperature and volume changes per unit mass, especially when studying phase transitions of substances like water. It contains three single-phase regions—liquid, vapor, and supercritical fluid—as well as a two-phase region (liquid + vapor). Additionally, it features two key curves: the saturated liquid curve and the saturated vapor curve, which define the boundaries of the two-phase region. When solids are considered, the number of regions and curves increases, providing a more detailed phase behavior representation.
What are P-v diagrams in thermodynamics?
A P-v diagram (pressure-volume plot) in thermodynamics is a graphical representation that illustrates the relationship between pressure (P) and the specific volume (v) of a system. In this diagram, pressure is plotted on the y-axis, while specific volume is plotted on the x-axis. Each point on the P-v diagram represents a different state of the gas, allowing for a clear visualization of how pressure and volume change during thermodynamic processes.
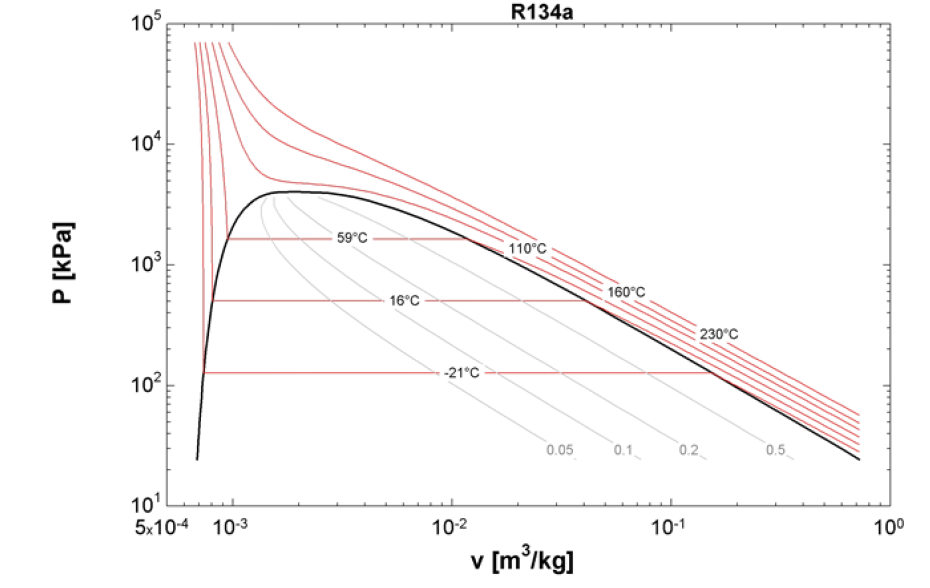
This diagram is particularly useful for analyzing work done by or on a gas during processes such as isothermal (constant temperature), adiabatic (no heat transfer), isobaric (constant pressure), and isochoric (constant volume) expansions and compressions.
What is a T-s diagram in thermodynamics with an example?
A T-s diagram (temperature-entropy plot) in thermodynamics is a graphical representation that illustrates the relationship between temperature (T) and entropy (s) of a system. In this diagram, temperature is plotted on the y-axis, while entropy is plotted on the x-axis, providing a useful tool for analyzing thermodynamic processes and cycles. The T-s diagram is particularly valuable in understanding heat transfer and work interactions, as well as identifying irreversibilities within a system.
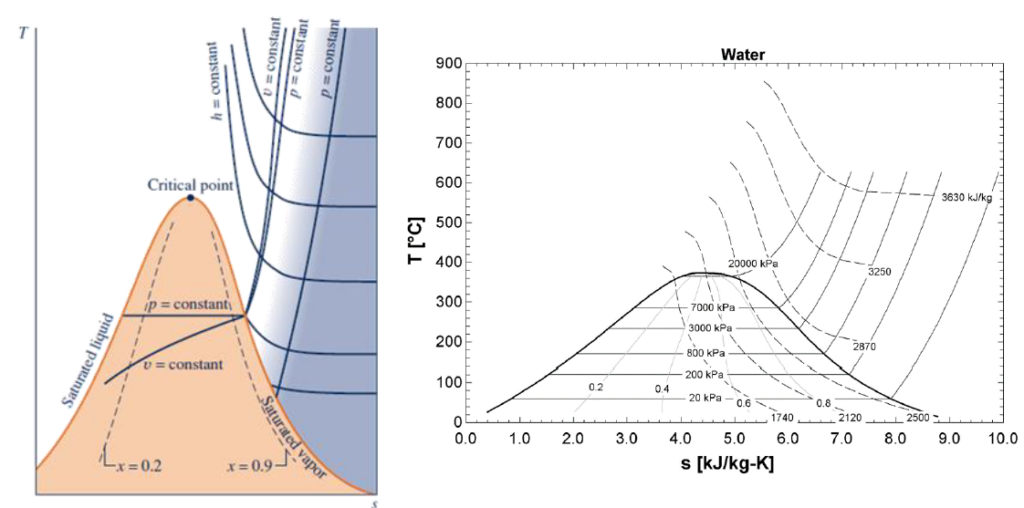
Example:
For an ideal gas, a T-s diagram at constant pressure shows that entropy increases as temperature increases. This behavior can be seen in thermodynamic cycles such as the Rankine cycle (used in steam power plants) and the Brayton cycle (used in gas turbines), where different process paths, such as isentropic (constant entropy) expansions and compressions, are visualized. By analyzing these cycles on a T-s diagram, engineers can evaluate the efficiency and performance of energy conversion systems.
Specific Heat
Specific heat is the amount of heat energy required to raise the temperature of a unit mass of a substance by one degree. There are two main types of specific heat: specific heat at constant volume (cv) and specific heat at constant pressure (cp).
cv represents the change in internal energy per unit change in temperature when volume remains constant, expressed as cv=(∂T/∂u)v . Similarly, cp represents the change in enthalpy per unit change in temperature when pressure remains constant, given by cp=(∂T/∂h)p.
In general, internal energy (u) is a function of pressure (P), volume (v), and temperature (T), while enthalpy (h) depends on pressure and temperature. Understanding specific heat is essential for analyzing energy transfer in thermodynamic processes, such as heating and cooling in gases and liquids.
Conclusion
Understanding the principles of thermodynamics is essential for analyzing and optimizing energy systems in various engineering and scientific applications. This crash course has covered key concepts, including the laws of thermodynamics, energy conservation, and work and heat interactions within a closed system, where energy can cross the boundary, but mass remains constant. By mastering these fundamentals, one can better comprehend processes such as heat engines, refrigeration cycles, and energy efficiency improvements.
Thermodynamic Equations






🎪 Roll up to the idea circus! Sprunki is your creative ringmaster.
I want studying and I think this website got some genuinely utilitarian stuff on it! .
Hello.This post was really interesting, particularly since I was investigating for thoughts on this matter last Sunday.