A Journey into Frequency Response, Filters and Resonance

Ever wondered how you can listen to your favorite song from the low thump of the bass to the twinkling highs of the cymbals? Or how your voice travels through phone lines, reaching a friend miles away with crystal clarity? It’s all thanks to the fascinating world of frequency response, Filters , and resonance – the secret ingredients that shape the way signals dance through our devices and systems.

What is meant by Fourier analysis?

Fourier analysis is utilized for detecting patterns or cycles within a normalized time series dataset. Picture a symphony orchestra getting ready to captivate its audience. Similar to a conductor assembling a diverse ensemble of musicians, signals consist of an array of frequencies. These frequencies, resembling the distinct tones of musical instruments, can be unveiled through the potent technique known as Fourier analysis – much like deconstructing a complex chord into its individual musical notes.

• All real-world signals are sums of sinusoidal components having various frequencies, amplitudes, and phases.

Diving into Square Waves and Sample Signals

Let’s think of a square wave as a rhythmic tap on a drum – it alternates abruptly between high and low states. Similarly, signals in the real world are usually continuous, but our devices need to interpret them in discrete steps. This is where sampling comes in, converting the continuous signal into digital chunks, much like capturing snapshots of a dancer mid-move.

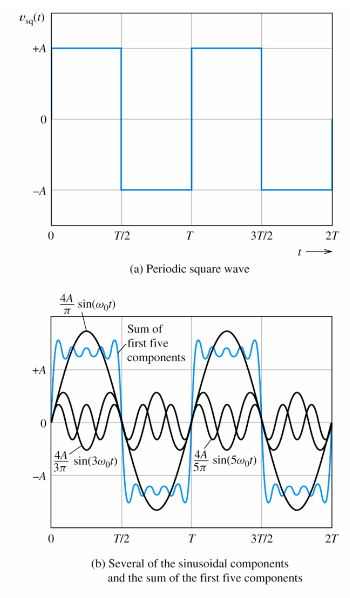
What signal uses square waves?

In the realm of digital systems, square waves serve as a foundational signal. Functioning as precise timing references or “clock signals,” their rapid transitions adeptly trigger synchronous logic circuits at predetermined intervals. These sharp shifts between high and low states are essential for encoding binary information, thus facilitating the operation of digital devices and communication protocols.

Behind the Scenes: How Filters Work

Filters are the stage managers of this signal symphony. Filters are designed to allow certain frequencies to pass through while removing unwanted frequency components from the signal to get a proper signal. It’s like having a DJ who only lets certain genres play at a party – filters tailor the signal’s sound according to their design.

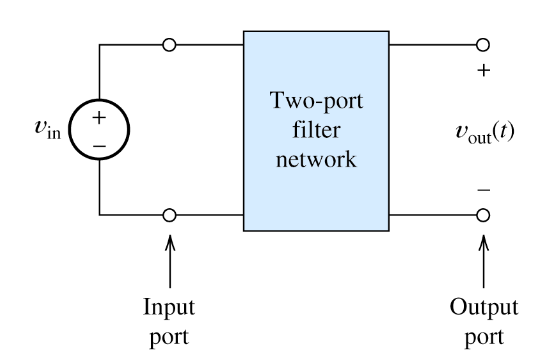
In the picture above when input signal v_in (t) is applied to the input port of a filter, some components are passed to the output port while others are not, depending on thier requencies. Thus v_out (t) contains some of the compoents of v_in (t) but not others. Usually, the amlitudes and phaes of the compoents are altered in passing though the filter.

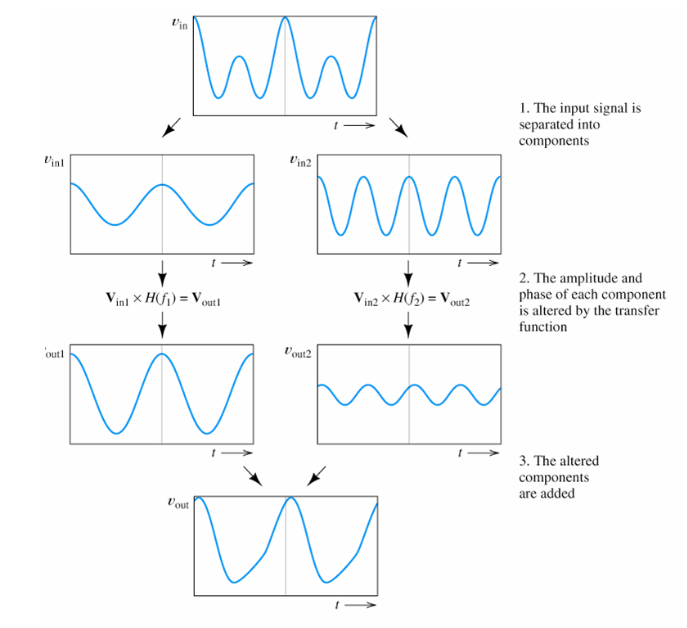
Steps to modify eletrical signals using a filter

1. Filters behave as if they separate the input into components
2. Modify the amplitudes and phase of each component
3. Add the modified components to produce output

Magnitude, Phase, and the Dance of Filters

The magnitude of the transfer function shows how the amplitude of each frequency component is affected by the filter, in other words it represents the volume of specific frequencies. Similarly, the phase of the transfer function shows how the phase of each frequency component is affected by the filter. Phase determines the alignment of those frequencies in relation to time, similar to how a dance instructor synchronized dance routine where each dancer’s steps are perfectly timed and aligned.

What is the transfer function of a filter?

The transfer function H(f) of the two-port filter is defined to be the ratio of the phasor output voltage to the phasor input voltage as a function of frequency:

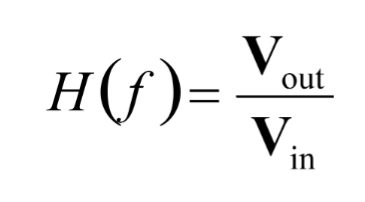
Transfer functions are the choreographers that guide this dance. Imagine a magician transforming a bouquet of flowers into a flock of doves – the transfer function works its magic to reshape the signal.

Measuring the Unseen: Capturing Transfer Functions

But how do we measure these transfer functions? To measure the transfer function, we apply a sinusoidal input singal, measure the amplitudes and phaes of input and output in steady state, and then divide the phasor output by the phasor input. The procedure is repeated for each frequency of intrest

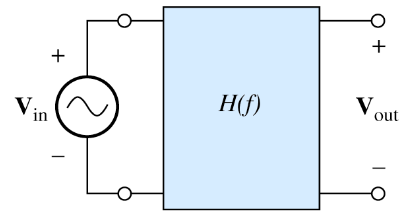
Just as a music producer tweaks knobs on a soundboard, engineers use input-output experiments to see how signals morph. This experimentation reveals the true nature of the signal’s behavior within a given system.

What is a first order low pass filter?

A first-order low pass filter is a basic electronic component that permits low-frequency signals to pass through while reducing the amplitude of higher frequencies. Think of a low pass filter as a velvet rope at a VIP party.  It helps to smooth out signals by removing sharp transitions and sudden changes in the waveform.

What are the equations for the low-pass filter?

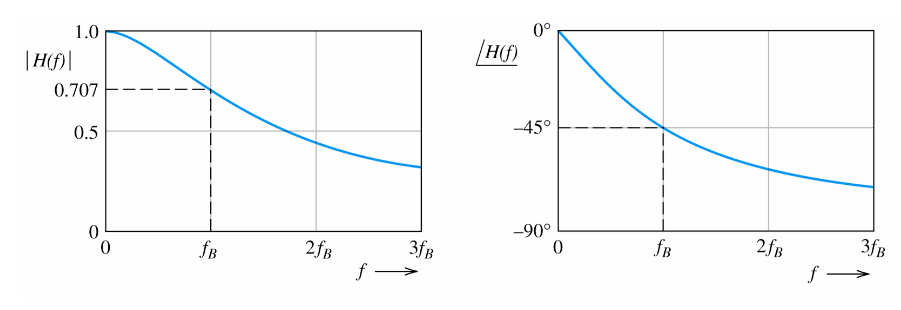
A low-pass filter’s cutoff frequency ƒ_b = 1/(2πRC). The phase angle of the output signal at ƒ_b and is -45^o for a Low Pass Filter.

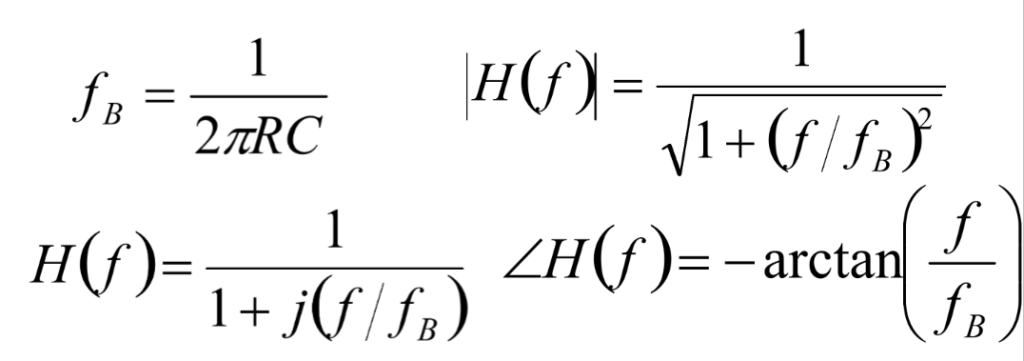
Magnitude and phase of the low pass filter transfer function

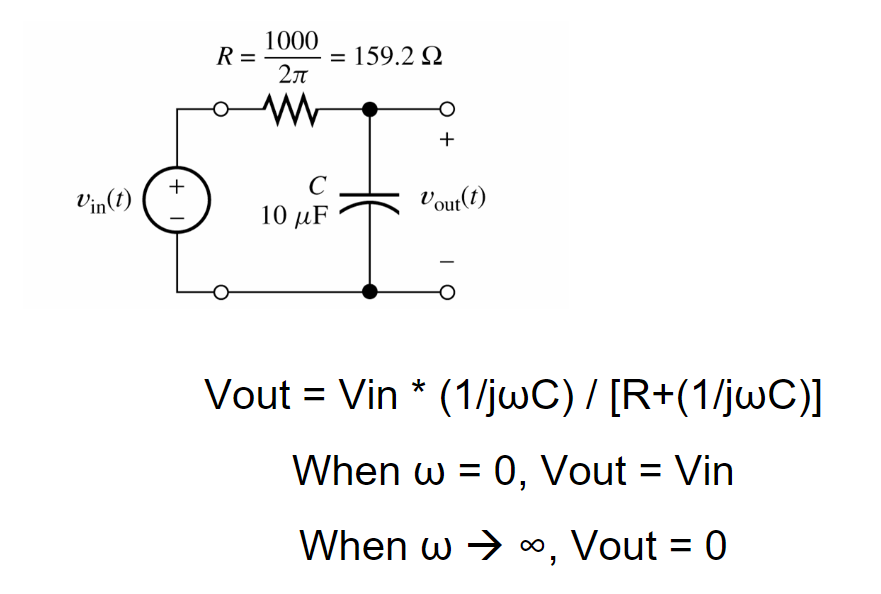
Example

Decibels and Logarithmic Frequency Scales: The Sonic Richter Scale

Ever heard of the term “decibel”? It’s the sonic cousin of kilometers per hour. Just as a car’s speed doesn’t increase linearly with its engine power, our perception of sound intensity isn’t linear either. In other words becuase the decibel scale is a logarithmic one, doubling the gain does not double the decibel value. Decibels and logarithmic scales help us make sense of this wild ride.

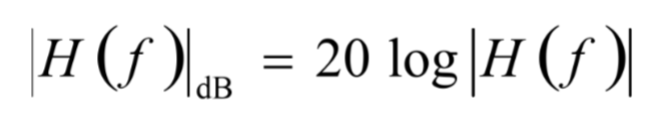
Transfer function and decibels

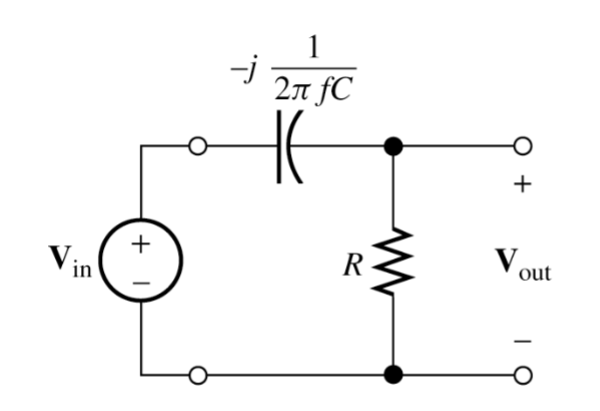
Raising the Curtain on First-Order High Pass Filters

Unlike a low pass filter a high pass filters lets high frequency signal gets pass but low frequency components get filtered.

In the intricate dance of signals, frequency response, Bode plots, and resonance come together to orchestrate the harmony we experience in the world of technology. Just as a conductor guides an orchestra to produce enchanting music, engineers manipulate these concepts to craft seamless communication and entertainment experiences.

What are the equations for the high-pass filter?

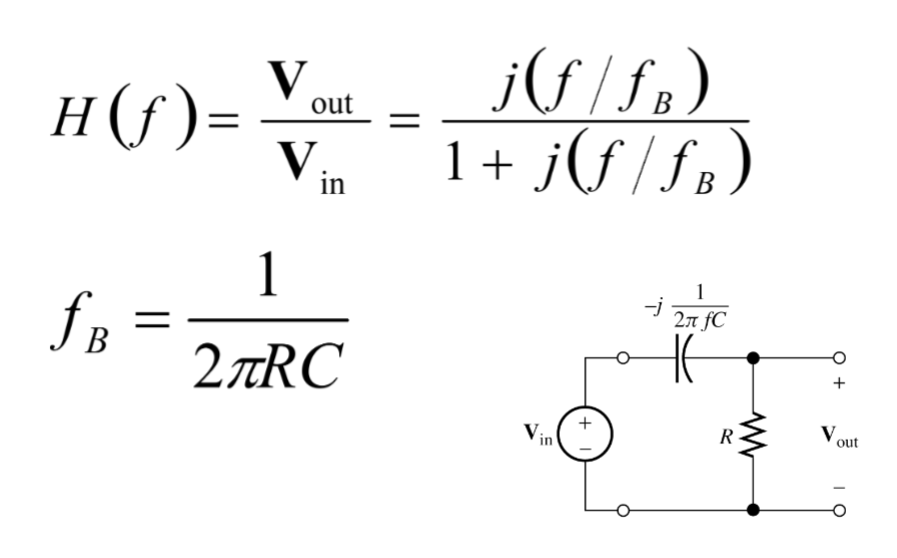
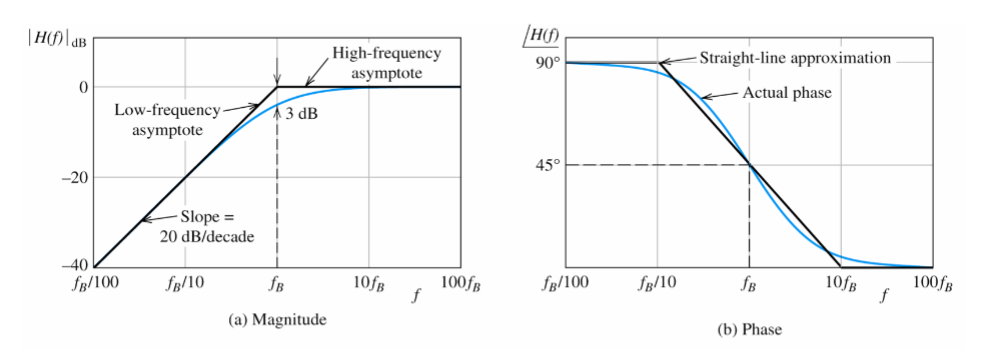
Magnitude and phase bode plot

The Bode Plot or Frequency Response Curve above for a high pass filter is the opposite to that of a low pass filter.

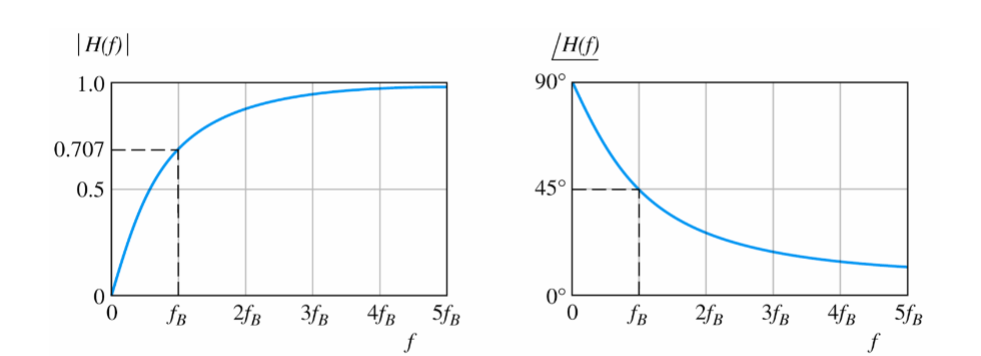
Bode plots of high pass

So, the next time you tap your foot to a beat, make a phone call or stream a movie, remember that it’s the result of signals following the rhythm set by frequency response, Bode plots, and the enchanting resonance of our technological symphony.

Conclusion

In the captivating realm of technology’s symphony, where signals dance and harmonize, we’ve embarked on a journey through the wondrous concepts of frequency response, Bode plots, and resonance. From Fourier analysis unveiling the orchestra of frequencies to filters sculpting the melodies of signals, we’ve explored the backstage magic that brings clarity to our communication and vibrancy to our entertainment. Transfer functions act as choreographers, guiding signals through intricate moves, while decibels and logarithmic scales provide the sonic Richter scale for our perceptions. With first-order low pass and high pass filters as smooth operators and energetic bouncers, we’ve uncovered how these ideas seamlessly blend to create the melodies of our technological world. So, as you witness the enchanting interplay of sound and information, remember that frequency response, Bode plots, and resonance are the composers of the symphony that connects us all.