Understanding Mechanical Waves
Mechanical waves are fundamental phenomena that play a critical role in various fields of science and engineering. They arise from disturbances that propagate through a medium such as a solid, liquid, or gas, transferring energy without transporting matter.
What are the main types of waves?
A wave refers to the transfer or flow of energy from one point to another in the form of oscillations that travel through a medium (either space or mass). To analyze wave propagation, it is essential to characterize the medium material. Waves can be categorized into three types based on the orientation of particle motion and the direction of energy:
- Mechanical waves
- Electromagnetic waves,
- Matter waves.
Types of Mechanical Waves
Mechanical waves are disturbances that propagate through a medium, transferring energy without transporting the medium’s material particles. They can be classified based on the direction of particle motion relative to the direction of wave propagation. Here are the three common types of mechanical waves:
Transverse Waves: In these waves, particles oscillate perpendicular to the direction of wave propagation. Examples include waves on a string, water waves, some seismic waves.
Longitudinal Waves: Here, particles oscillate parallel to the wave’s direction. P-waves in seismology and sound waves.
surface waves: Travel along the surface of a medium and have complex particle motion.
Wave Properties and Equations
Mechanical waves are characterized by several key parameters:
- Wavelength (λ): The spatial length of one complete wave cycle (in m).
- Frequency (f): The number of cycles per second, measured in Hertz (Hz). Hz = 1 (complete wave or oscillation or cycle)/s = 1 s–1.
- Period (T): The time required for one complete cycle (in s) , inversely related to frequency (𝑓=1/T).
- Wave Speed (υ): Determined by the equation υ= 𝜆𝑓. wave speed is measured in (in m/s ) and it defines how fast the wave travels through the medium.
The angular frequency (ω) and wave number (k) are additional metrics derived as:
The scalar quantities ω and k are also never negative. The “2π” in these two equations is 2π radians. The two equations above allow wave speed to also be expressed as: υ = ω/k.
Sinusoidal Wave Functions
A sinusoidal function is a type of periodic function that smoothly oscillates between maximum and minimum values, following the shape of a sine wave. It can also be represented using a cosine function, as cosine is simply a horizontally shifted version of the sine function.
The sine of any angle ranges from -1 to +1. For instance, the sine of 0 degrees is 0, the sine of 90∘ degrees is 1, and the sine of 270 degrees is -1. By the time we reach 360 degrees, the sine returns to 0. A cosine wave is offset by 90 degrees in phase relative to a sine wave.
The cosine of 0 degrees is 1, and the cosine of 90 degrees is 0, indicating that a cosine wave is 90 degrees out of phase with a sine wave. Multiple sine waves can coexist simultaneously, each with varying angular phase differences relative to one another. When referring to a phase angle, it is always described as another reference point.
What is a sine wave, and how does it relate to natural phenomena and applications?
A sine wave, or sinusoidal wave, is a natural way to represent how various phenomena in nature change over time. It illustrates how the amplitude of a variable, such as audible sound, varies with time. For instance, a single pure musical note corresponds to a sine wave, though it would sound flat and plain without the harmonics typically present in natural sounds. Similarly, a simple oscillating or alternating current or voltage in a wire can also be described by a sine wave.
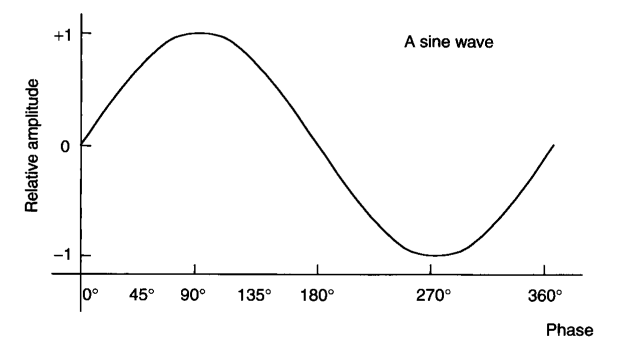
We now consider the sinusoidal functions of x and t, y(x,t), for waves. At the origin (where x = 0), let y(0,t) = A cos ωt. For waves moving in the +x-direction, at some position x (in m) and time t (in s), we have a displacement component y(x,t) that occurred at the origin. The displacement of a sinusoidal wave in space and time is expressed mathematically as:
y(x,t)=Acos(kx−ωt) (for sinusoidal waves moving in the +x direction)
y(x,t)=Acos(kx+ωt) (for sinusoidal waves moving in the -x direction)
where A represents the wave’s amplitude, indicating the maximum displacement from equilibrium. The signs in the phase expression can be adjusted to account for wave direction.
For a particle in the medium:
- Its displacement component from equilibrium is y(x,t) = A cos (kx ± ωt).
- Its velocity component is υy = ∂y/∂t = ±ωA sin (kx ± ωt), so (υy)max = ωA.
- Its acceleration component is ay = –ω2A cos (kx ± ωt) = –ω2y, so (ay)max = ω2A.
Energy Transmission and Wave Speed in Strings
If we move along with the crest of a wave, we observe the string (or wire, cable, rope, or spring) moving past us at the wave speed (υ). A small segment of the crest, of length L, can be closely approximated as part of a circle with radius R. The weight of this segment is negligible, allowing us to simplify the force equation ΣFy=may to −2Fsinθ=m(−υ2/R). Since θ is very small, sinθ can be approximated as θ (in radians), where θ=L/2R. Additionally, the mass of the segment is given by m=μL, where μ is the linear mass density. Substituting these relationships into the force equation simplifies it to:
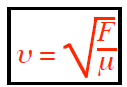
Where:
υ is the wave speed (in m/s ) on the string (or wire or cable, rope or spring, etc.).
F is the magnitude of the tension (in N), which is the force stretching the string/ rope/etc.
μ is the mass per length, m/L (in kg/m, NOT g/m) of the string/ rope/etc. Note that L is NOT the self-inductance. Also note μ is NOT the metric prefix 10-6, NOT the magnetic dipole moment NIA, and NOT the permeability.
The average power (Pav) transmitted by sinusoidal waves is:
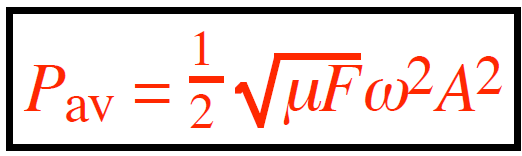
where:
Pav is the average power (in W = watt) carried by a transverse sinusoidal wave moving along a string/ rope/etc.
Interference and Standing Waves
A traveling wave moves from one location to another. When a traveling wave on a string/rope/etc. reaches a fixed end, it reflects and inverts, undergoing a phase change of π radians. Conversely, if the wave encounters a free end, it reflects without inversion, resulting in no phase change.
For linear materials, the principle of superposition applies: when two or more waves overlap, their resulting displacement is the vector sum of the displacements of the individual waves.
- Constructive Interference: Increased amplitude when wave crests align.
- Destructive Interference: Reduced amplitude when a crest aligns with a trough.
- Node: is a point of zero motion (no displacement).
- Antinode: a point of maximum magnitudes of motion and displacement.
Standing waves form when two identical traveling waves moving in opposite directions interfere. Their displacement is described by:
Here A is the amplitude (in m) of either traveling wave and 2A is the amplitude (in m) of
the standing wave at its antinode(s).
Nodes (points of no displacement) and antinodes (points of maximum displacement) characterize standing waves, with specific spatial relationships:
- Distance between a node and the nearest antinode: λ/4
- Distance between two consecutive nodes or antinodes (if they exist): λ/2
How is data transmitted in waves?
Data is transmitted in waves by modulating certain properties of a carrier wave, such as amplitude, frequency, or phase, to encode information. For digital data, binary ‘ones’ and ‘zeroes’ can be represented using phase modulation, where two signals of the same amplitude and frequency are shifted in phase relative to each other or a reference marker.
In wireless communication, radio waves serve as the carrier for transmitting information. The data is imposed on the carrier wave using methods like amplitude modulation (AM), frequency modulation (FM), or pulse modulation for digital signals. These techniques enable the transmission of sound, messages, and other information over distances for purposes such as communication, navigation, and more.
