Electromagnetic Induction and Maxwell’s Equations
Electromagnetism lies at the heart of many modern technologies, from power generation to wireless communication. Its foundational principles are electromagnetic induction and Maxwell’s Equations, which describe the dynamic interplay between electric and magnetic fields.
Electromagnetic induction explains how changing magnetic fields produce electric currents, a phenomenon first uncovered by Michael Faraday. Meanwhile, Maxwell’s Equations provide a unified framework for understanding the behavior of electric and magnetic fields, revealing their interconnected nature and their role in wave propagation. This article delves into these pivotal concepts, offering insights into their principles, applications, and impact on science and technology.
Faraday’s Law of Induction
One of the pivotal principles in electromagnetism is Faraday’s Law of Induction. In 1831, Michael Faraday discovered that an electric field could be generated by varying the magnetic field with time. This phenomenon is known as electromagnetic induction.
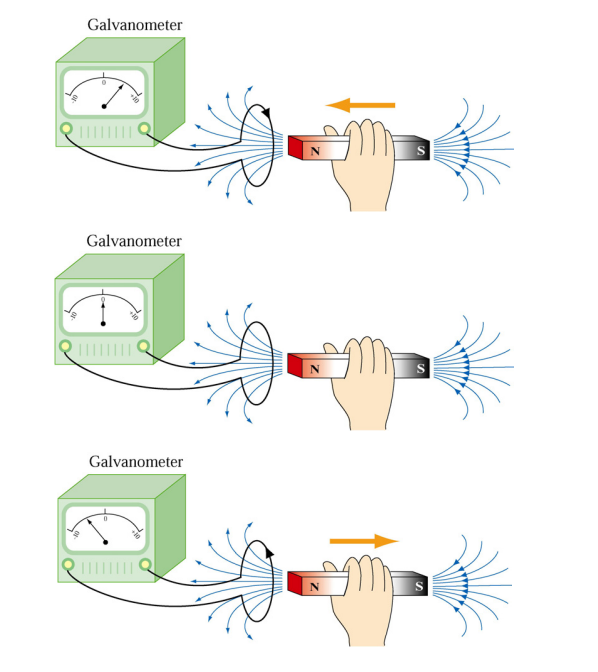
Faraday’s experiment revealed that no current is detected in the galvanometer when a bar magnet remains stationary relative to a loop. However, when there is relative motion between the magnet and the loop, a current is induced. The galvanometer deflects in one direction as the magnet approaches the loop and in the opposite direction as it moves away. This demonstrates that a changing magnetic field induces an electric current in the loop, effectively behaving as though connected to an EMF source. The induced emf is directly related to the rate at which the magnetic flux through the coil changes.
What is EMF in simple words?
Electromotive Force (EMF) is the voltage generated by a source, such as a battery or generator, that drives electric current in a circuit. It represents the source’s ability to convert energy from one form (like chemical or mechanical energy) into electrical energy. EMF is measured in volts and can result from electrochemical reactions, time-varying magnetic fields, or other processes that create an electric potential difference.
What is Faraday’s Law of Induction?
Faraday’s Law of electromagnetic induction states that an electromotive force (EMF) is induced in a closed circuit whenever the magnetic flux through the circuit changes. The magnitude of the induced EMF is directly proportional to the rate at which the magnetic flux varies.

Here:
- ε represents the induced electromotive force (emf) in volts (V) —a potential difference that may give an induced current.
- N is the number of turns in a coil (no unit).
- ΦΒ is the magnetic flux in Weber (Wb), representing the average magnetic field passing through the coil.
- dΦΒ/ dt is the rate at which ΦΒ is changing with time (in Wb/s ). Thus 1 Wb/s = 1 V
The rate of change of magnetic flux (ΦΒ) induces an emf, a concept central to electric generators and transformers.
Lenz’s Law
Closely tied to Faraday’s Law, Lenz’s Law dictates that the direction of the induced emf opposes the change causing it. This principle ensures the conservation of energy and can be summarized as:
The induced current flows in such a direction that it opposes the change in magnetic flux.
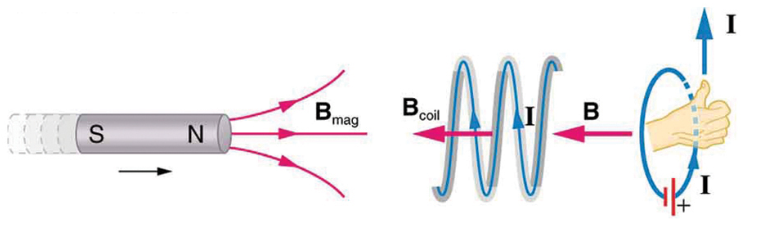
Motional emf
The motional emf is a specific case of induced emf, given by:

Where:
- ε is the (motional) emf (in V)
- υ⊥, Β⊥, and l⊥are the mutually perpendicular components of velocity, magnetic field, and straight segment length.
Since the emf is a potential difference, and a potential difference equals the integral of E·dl, for a single
loop Faraday’s law of induction becomes:

Where:
- E is the induced electric field (in V/m or N/C ).
What is the difference between Lenz’s law and Faraday’s law?
Lenz’s Law determines the direction of an induced current, while Faraday’s Law explains the magnitude of the induced electromotive force (EMF) based on the rate of change of the magnetic flux that causes it.
Together, these laws provide a comprehensive understanding of electromagnetic induction. Faraday’s Law explains how and why EMF is generated, while Lenz’s Law describes the direction of the induced EMF and its opposition to changes in magnetic flux.
Displacement Current and Ampere’s Law
It’s important to remember that eddy currents are induced currents that circulate within the volume of a conducting material. Maxwell resolved inconsistencies in Ampere’s Law by introducing the concept of displacement current, iD. Maxwell’s introduction of displacement current unified electricity and magnetism, showing that they are two aspects of the same phenomenon. The displacement current is not an actual motion of charge but has the SI unit of ampere = amp = A. Note iD = 0 only if the electric flux ΦE is constant.

Where:
- ε is the permittivity (in C2 /N·m2 or F/ m ).
- ΦE is the electric flux (N·m2 / C or V·m).
- dΦE/ dt is the rate at which the electric flux changes with time (in N·m2 / C·s or V·m/s)
Thus, when no magnetic materials are present, Ampere’s law becomes:
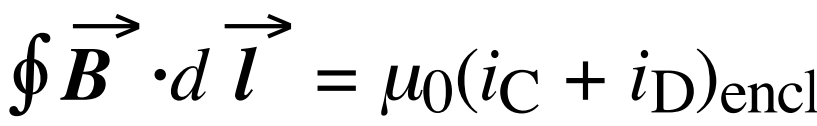
Where:
- iC is the enclosed conduction current (in A) (caused by actual charge motion).
- iD is the enclosed displacement current (in A) (caused by changing enclosed electric flux).
This form accounts for the changing electric flux in capacitors and ensures the continuity of electromagnetic theory.
What are the 4 Maxwell’s equations?
Maxwell’s four fundamental equations describe the behavior of electric and magnetic fields. These equations are essential in electromagnetism and are named after the physicist James Clerk Maxwell. The four equations are:

What do Maxwell’s equations tell us?
Maxwell’s equations provide a comprehensive framework for understanding how electric charges and currents generate electric and magnetic fields and how these fields interact and evolve. They are fundamental to electromagnetism and have far-reaching implications in physics and engineering. Here are the key insights from Maxwell’s equations:
- Electric Charges and Fields: Gauss’s Law relates the distribution of electric charges to the electric field they create. It explains how charges serve as sources or sinks of the electric field.
- Magnetic Fields and Monopoles: Gauss’s Law for Magnetism states that magnetic field lines form closed loops, implying the absence of magnetic monopoles. This highlights the fundamental difference between electric and magnetic fields.
- Field Interactions: Faraday’s Law of Induction describes how a changing magnetic field generates an electric field. Ampère’s Law (with Maxwell’s correction) explains how a changing electric field and electric currents produce a magnetic field. Together, these laws illustrate the interplay between electric and magnetic fields.
- Temporal Evolution: Maxwell’s equations describe how electric and magnetic fields change over time in response to charges and currents, providing a dynamic picture of these fields.
- Wave Propagation: They explain the propagation of electromagnetic waves, such as light and radio waves, through space. This insight is essential for understanding the behavior of all forms of electromagnetic radiation.
Inductance and Energy Storage
An inductor (sometimes called a choke) is a circuit element used mainly for its inductance. Consider a single coil, a varying current within the coil generates a changing magnetic field, which in turn results in a varying magnetic flux through the coil. According to Faraday’s Law of Induction, this process induces a self-induced emf ε (in volts).
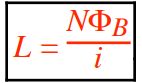
The equation above represents the coil’s self-inductance (in Henries, H), commonly referred to as inductance. In the expression above, all the quantities are inherently non-negative.
Similar to using U = 0.5CV2 and a parallel-plate capacitor to find the energy density u of an electric field, we now use U =0.5LI2 and a toroid to find the energy density u of a magnetic field. Consider a toroid of a small cross-section and two layers of wire wound so that its magnetic field is zero outside the “dough” of its doughnut-shaped core.
What is the energy density in a magnetic field?
The energy density in a magnetic field is:
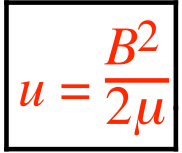
Here:
- u is the energy density (in J/m3 ) of the magnetic field B (in T) .
- is the magnetic field strength.
- µ (mu) is the material’s permeability (in T·m/A ).
- µ0 is the permeability of vacuum(µ0 ≡ 4π × 10–7 T·m/A ).
Thus µ ≡ µ0 by definition for vacuum and also for nonmagnetic materials. Because of their ordinarily weak magnetizations, µ is slightly greater than µ0 for paramagnetic materials (if not at very low temperatures) and µ is slightly less than µ0 for ordinary diamagnetic materials (not superconducting).
Be careful to distinguish between U (magnetic potential energy), u (energy density), and µ (permeability).
Practical Applications
The principles of electromagnetic induction and Maxwell’s Equations underpin many technologies, including:
- Electric generators and transformers.
- Wireless communication systems.
- Magnetic resonance imaging (MRI).
- Inductive charging systems.
By mastering these foundational principles, one gains a profound understanding of the dynamic interplay between electricity and magnetism, enabling the development of cutting-edge technologies.
Conclusion
Understanding electromagnetic induction and Maxwell’s Equations is essential to grasp the fundamental mechanisms behind electric and magnetic phenomena. These principles not only underpin the development of technologies such as electric generators, transformers, and wireless communication systems but also provide critical insights into the nature of electromagnetic waves, including light.
By bridging theoretical physics with practical applications, these concepts continue to drive innovation across multiple scientific and engineering disciplines. As our understanding of electromagnetism deepens, the potential for breakthroughs and technologies rooted in these timeless laws remains boundless.






