Circuit Simplification: Norton Equivalent and Source Transformations

Today, I want to talk about something about some circuit simplification techniques. I know circuits can be confusing and overwhelming, but by understanding a few key concepts like Norton equivalent and source transformations, you’ll be able to simplify circuits like a pro.

How do you simplify circuits?

Have you ever looked at a circuit and felt like it was a jumble of wires and components? Well, that’s where circuit simplification techniques come to the rescue. These techniques help us simplify complex circuits into more manageable forms, making them easier to analyze and understand. A few commonly used techniques are Norton and Thevenin equivalent circuits (TEC) and source transformations.

Why is Norton’s theorem useful?

Imagine you have a complex circuit with multiple resistors, voltage sources, and current sources. Determining the current flowing through a particular branch of the circuit can be challenging. That’s where the Norton equivalent comes into play.

Norton’s Theorem allows us to simplify a complex circuit by replacing the entire network of resistors, and voltage/current sources with a single current source in parallel with a single resistor. This equivalent circuit behaves the same as the original circuit from the perspective of an external load. The Norton equivalent circuit consists of an independent current source I_n in parallel with the Thevenin resistance R_th.

The Norton current is the total current entering the short circuit across the load terminals, while the Thevenin resistance is the resistance between those terminals when all the independent sources are deactivated. By calculating these values, we can represent the original circuit with just a few components, making it easier to work with.

Example

What is meant by source transformation?

Now, let’s talk about source transformations. Source transformations allow us to convert voltage sources into equivalent current sources and vice versa. The method is based on Thevenin’s theorem and Norton’s theorem.

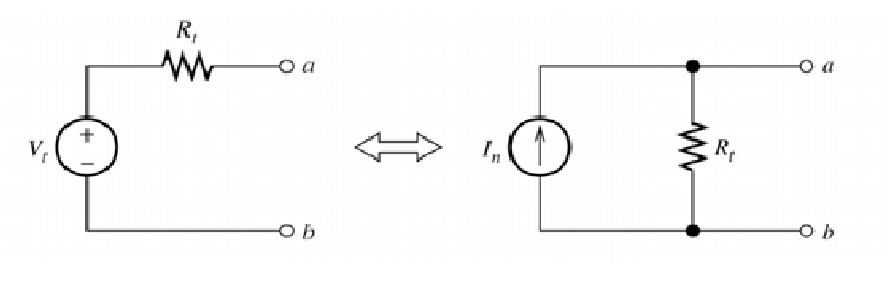
To perform a source transformation, we replace a voltage source with a current source or vice versa while maintaining the same behavior of the circuit. This transformation is based on Ohm’s Law and the relationship between voltage, current, and resistance.

Example

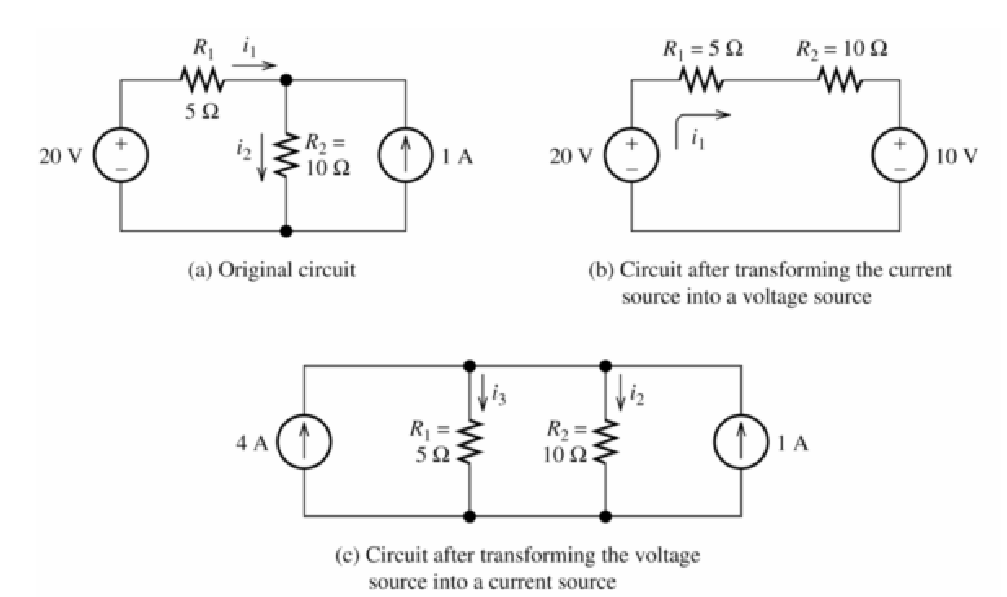
Applying Norton Equivalent and Source Transformations

Okay, now that we understand the basic concepts, let’s see how we can apply Norton equivalent and source transformations to simplify circuits.

How do you calculate Norton equivalent circuit?

**Note the similarity between the steps to find a Norton equivalent circuit and a Thevenin Equivalent Circuit**

1. Perform two of these:
   • Determine the open circuit voltage V_th= v_oc.
   • Determine the short circuit current I_n = i_sc.
   • Zero the sources and find the Thevenin resistance R_th looking back into the terminals.
2. The Thevenin equivalent consists of a voltage source V_th in series with R_th.
3. The Norton equivalent consists of a current source I_n in parallel with R_th .

How do you solve source transformation?

1. Identify the voltage source or current source that can be transformed.
2. If converting a voltage source to a current source, divide the voltage value by the resistance connected to the source. The resulting current will be the equivalent current source.
3. If converting a current source to a voltage source, multiply the current value by the resistance connected to the source. The resulting voltage will be the equivalent voltage source.
4. Replace the original source with the equivalent source.

Limitations and Considerations

While Norton equivalent and source transformations are powerful tools for circuit simplification, it’s essential to be aware of their limitations and consider certain factors before applying them.

1. Nonlinear components: These techniques are primarily suitable for linear circuits. Nonlinear components, such as diodes or transistors, may not behave as expected and can limit the effectiveness of these simplification techniques.
2. Time-domain analysis: Norton equivalent and source transformations are most commonly used for steady-state analysis. If you’re dealing with circuits that involve time-varying signals or transient behavior, additional techniques may be required.
3. Accuracy: Although these techniques simplify the circuit, they can introduce a certain degree of approximation. It’s important to evaluate the trade-off between circuit complexity and the accuracy required for your specific analysis.

Considering these factors and understanding the nature of your circuit will help you determine if Norton equivalent and source transformations are suitable for simplifying your particular circuit.

Conclusion

Congratulations! You’ve now learned about two powerful circuit simplification techniques: Norton equivalent and source transformations. By applying these techniques, you can simplify complex circuits, making them easier to analyze and understand.

Remember, circuit simplification is not just about finding the shortest route to the solution but also about gaining a deeper understanding of circuit behavior. So, don’t be afraid to experiment and explore different techniques.