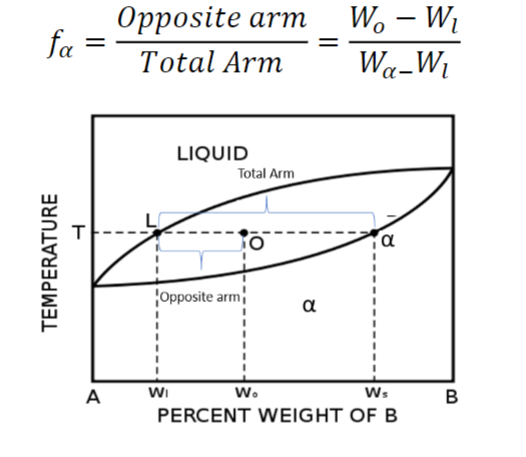
Inverse lever Rule Explained

You might be asking yourself why should you care about the inverse lever rule. If an alloy contains multiple phases, the lever rule can be used to determine the proportions of each phase. This rule is analogous to a simple balance, where the composition of the alloy acts as the fulcrum, and the compositions of the phases represent the ends of a bar. The weights required to balance the system correspond to the proportions of the phases present.

When should the inverse lever rule be used? And what does it state? How it should be used?

Derived from the conservation of mass, the lever rule is an equation that can be used to determine the overall composition of two metals with coexisting phases at a set point (both liquid and solid metal). Using the two following equations you can derive the lever rule:

1. The total mass of the alpha phase plus the total mass of the liquid phase is equal to the total mass of the alloy.
2. The fraction of alpha in the alloy and the fraction of liquid in the alloy must be equal to 1 since those two are the only two compounds in the alloy.

Using those two equations you can derive the lever rule. The weight percent of two coexisting phases at a point inside the two-phase region is inversely proportional to the gap between the intersection point to the boundary line divided by the total tie arm.

Imagine the tie-line (Line LOα) to be a seesaw with point O to be the fulcrum. Line LO is the liquid arm and line Oα is the alpha arm. So if you were trying to determine the weight percent of alpha you would just divide the liquid arm (opposite arm) by the total arm or tie line. See the equation and graph below.