Sound and Electromagnetic Waves
Waves are fundamental to our understanding of the physical world, carrying energy and information across vast distances. Among the many types of waves, electromagnetic waves stand out for their versatility and profound impact on science and technology. These waves, including visible light to X-rays and radio waves, are essential to countless applications in daily life, from communication and healthcare to energy and exploration.
This article delves into the fascinating world of Sound and electromagnetic (em) waves, exploring the principles that govern their behavior, including wave properties, the Doppler effect, and radiation pressure. We will also examine how James Clerk Maxwell’s groundbreaking work unified the understanding of electric and magnetic fields, laying the foundation for modern electromagnetism. By understanding these concepts, we gain insights into the forces that shape our universe and enable many of the technologies we rely on today.
The Doppler Effect for Sound
The Doppler effect refers to the change in frequency perceived when a source and an observer are in motion relative to each other. A common example is an ambulance passing by: the siren sounds higher in pitch as it approaches and lower as it moves away.

We examine the Doppler effect for sound in a scenario limited to one dimension, with no wind and a source emitting a single frequency (fS). This phenomenon explains how the frequency of sound changes based on the relative motion between the source and the listener.
Frequency Shift
When a listener and source move closer, the listener hears a higher frequency (fL>fS); when moving apart, the frequency decreases (fL<fS). Note that when the relative speed is zero, fL = fS.
Key Equation
We choose the direction from listener to source as positive to write just one equation for nine possibilities.
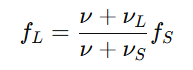
Here, ν is the speed of sound, νLand νS are the velocities of the listener and source, respectively. All three υ’s must have the same unit (m/s in SI).
Shock Waves
If the source moves faster than the speed of sound (∣νS∣>ν), it produces a shock wave. When |υS| and υ
are constant and the source is moving in a straight line, in three dimensions this shock wave is cone-shaped. This shock-wave cone makes an angle α with the straight-line path of a supersonic object.
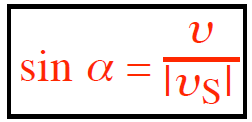
where the speed of sound υ and the speed of the supersonic source |υS| are both positive and have the same unit (m/s in SI).
Mach number
The Mach number (M or Ma), commonly referred to simply as Mach, is a dimensionless quantity in fluid dynamics that represents the ratio of an object’s flow velocity relative to a boundary to the local speed of sound. It is named after Austrian physicist and philosopher Ernst Mach.
The reciprocal of the right side of this equation, ∣νS∣ / ν, is known as the Mach number, with sin α = Mach number-1, the equation accounts for the absolute value of the source velocity.
Electromagnetic Waves
An electromagnetic (em) wave is a disturbance in electric and magnetic fields that propagates through space, carrying energy from one location to another. It is characterized by properties such as wavelength, amplitude, frequency, and phase. Electromagnetic waves span a broad range of frequencies, creating a spectrum that is divided into various types based on their frequency ranges.
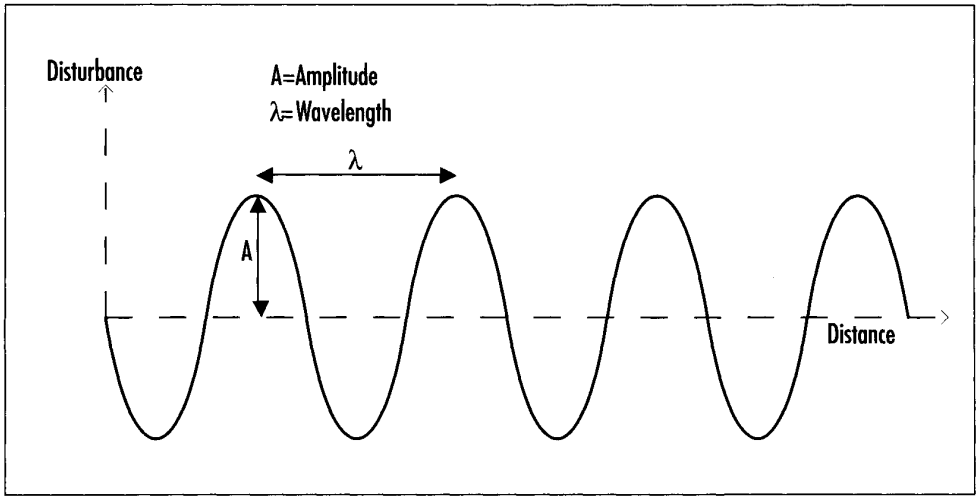
Electromagnetic waves are transverse waves, meaning the electric and magnetic fields oscillate in planes perpendicular to the direction of wave propagation. Additionally, the electric and magnetic fields are also perpendicular to each other.
Properties of Electromagnetic Waves
Oscillations: Electric fields (E⃗) and magnetic fields (B⃗) oscillate perpendicular to each other and the wave’s velocity direction.
Polarization: All E⃗ fields oscillate along the same line for linearly polarized waves, and B⃗ fields are perpendicular.
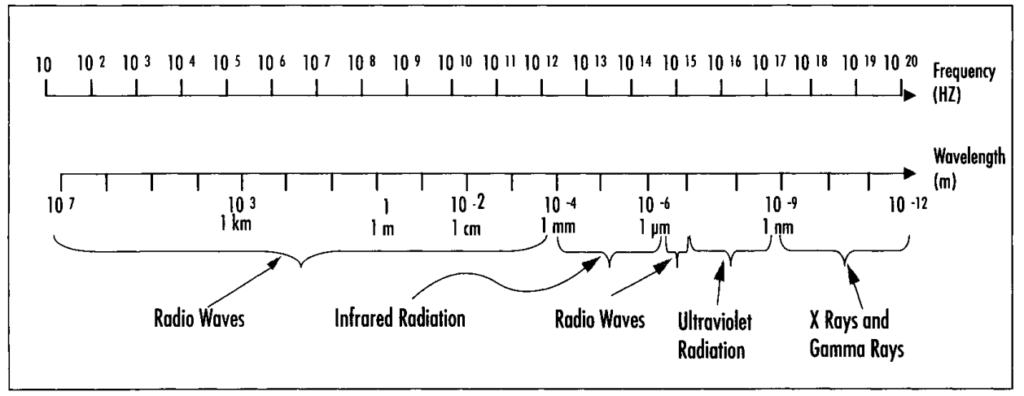
Electromagnetic spectrum: In order of increasing frequency (that is, decreasing wavelength), the electromagnetic spectrum has bands of radio waves, microwaves, infrared, visible light [λ0 = 700
nm (red) to λ0 = 400 nm (violet)], ultraviolet, x rays, and gamma rays.
Energy and Propagation
- The relationship between E⃗ and B⃗: Applying Maxwell’s equations to an em wave in a dielectric gives E=νB. In a vacuum, ν=c, the speed of light (3.00×108 m/s).
- where E (in V/m or N/C ) is the magnitude of the em wave’s electric field at some position and time
- B (in T) is the magnitude of the em wave’s magnetic field at the same position and at the same time.
- Energy density:
- Magnetic field energy: uB=B2/2μ
- Electric field energy: uE=1/2ϵE2 These are equal for an em wave.
What is the wave equation for Maxwell’s equation?
In 1864, James Clerk Maxwell unified the fundamental principles governing electric and magnetic fields by consolidating the four basic laws. By modifying Ampere’s law, he developed a comprehensive theory that interconnected electric and magnetic phenomena. These foundational principles are now known as Maxwell’s equations.
Maxwell found that these four equations have wavelike solutions and showed that the speed of electromagnetic waves equals the speed of light. This led him to conclude that light is an electromagnetic wave. Thus, Maxwell’s research not only united electricity and magnetism, it also laid a theoretical foundation for many optical phenomena Maxwell’s equations describe wave velocity (ν) in a dielectric as:

In a dielectric:
In a dielectric, ε = Kε0 and μ = Kmμ0. Also, Km = 1 and μ = μ0 for nonmagnetic materials and μ ≈ μ0 and Km ≈ 1 near and above room temperature for diamagnetic and paramagnetic materials.
- ϵ is the permittivity (in F/m ) of the dielectric, where ϵ0=8.854×10−12 F/m (vacuum permittivity).
- μ is the permeability (in T·m/A ) of the dielectric; μ0 is the permeability (in T·m/A ) of vacuum (μ0 ≡ 4π × 10–7 T·m/A ).
- K is the dielectric constant (no unit) of the dielectric and Km is its magnetic counterpart (no unit).
In a vacuum:
ϵ=ϵ0, μ=μ0, K=1, Km=1, ν=c, as a result, the values in the air are approximately equal to those in a vacuum. So the equation above can be simplified:
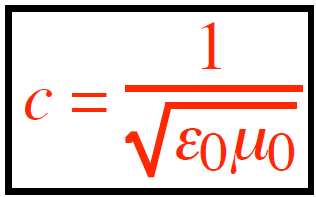
Intensity and Radiation Pressure
Electromagnetic radiation exerts pressure on a surface when it strikes it, a phenomenon known as radiation pressure.
Poynting vector
The Poynting vector is a fundamental concept in electromagnetism, representing the directional energy flux density of an electromagnetic field. The Poynting vector (S⃗) describes the energy flow of an electromagnetic (em) wave and is defined as:

Therefore, in the special case of vacuum (≈ air), μ can be replaced with μ0.
- Magnitude: The magnitude of S⃗ is given by ∣E⃗×B⃗∣=EB, measured in watts per square meter (W/m2).
- Direction: Thus the direction the wave is moving in the direction of E × B, that is, perpendicular to both E (electric field) and B (magnetic field).
The Poynting vector has various applications, including its extensive use in studying plane waves and more complex waveforms such as Laguerre–Gaussian beams, which exhibit helical wavefronts. Additionally, it plays a crucial role in Poynting’s theorem, which deals with energy conservation in electromagnetic fields.
What is the intensity of electromagnetic waves?
The ability of electromagnetic waves to transfer energy becomes unmistakable to anyone who spends too much time in the sun. This energy transfer is quantified by wave intensity, which describes the rate at which sunlight and other electromagnetic waves deliver energy.

For sinusoidal em waves, the intensity I is the average magnitude of the Poynting vector Sav, giving
(in a dielectric). The average power per unit area of the wave, given by: I =E2max / 2μc
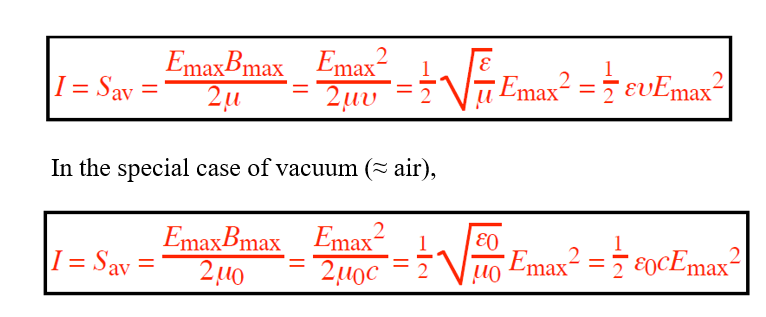
Recall that intensity I is the average power transmitted by the wave per perpendicular area and is thus in
W/m2.
What is meant by radiation pressure?
Radiation pressure refers to the mechanical pressure exerted on a surface due to the exchange of momentum between an electromagnetic field and the object. This momentum transfer occurs when photons collide with the surface of the object.
Radiation Pressure (prad): is the average pressure (in Pa = pascal) exerted by an em wave on a surface, it depends on whether the wave is absorbed or reflected:
prad=I/C (absorption) prad=2I / C(reflection)
Recall that pressure is the perpendicular force per area. The equations above are for an em
wave that hits normal (perpendicular) to a surface in vacuum (≈ air).
Standing Electromagnetic Waves
Standing Electromagnetic Waves are a form of wave pattern that results from the superposition of two opposite traveling waves of the same frequency. They create nodes and antinodes at fixed points along the wave, hence the term ‘standing’ as they appear to be standing still. Oppositely directed em waves of the same amplitude, frequency, wavelength, and polarization combine to produce standing waves.
Allowed frequencies and wavelengths between reflecting walls depend on the separation L (in m):
fn=ν/λn=nν/2L(n=1,2,3,…)
the allowed frequencies and wavelengths are fn (in Hz) and λn (in m) respectively. In the special case of
vacuum (≈ air) between the walls, υ ≡ c, so
fn=c/λn=nc/2L(n=1,2,3,…)