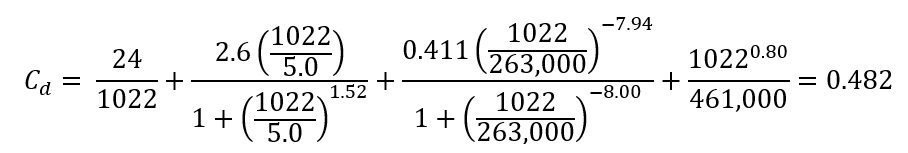Drag Forces Acting on Objects in a Wind Tunnel
Abstract:
This laboratory investigates how the drag coefficient changes with respect to Reynolds number Cd(Re) for a smooth sphere and a sphere with bumps. The bumps on the sphere were modeled by adding a rubber band on the sphere. The sphere was placed in a wind tunnel which carefully controls and monitors the airflow so the forces/pressure acting on the sphere can be measured. To calculate the coefficient of drag on each of the spheres the following equation was used,
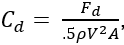
Where Cd is the coefficient of drag [-], Fd is the drag force [N], ρ is the density of the air [kg/m3], and A is the projected area [m2]. The results from this experiment show that at lower Reynolds number (1000-3000) the coefficient of drag is higher for the ball with the band. The two curves begin to converge between Reynolds numbers 3000 – 5000. For the small ball once the Reynolds number reached 5000 the graph had actually flipped, where the ball with the band had a lower coefficient of drag then the ball with no band. Both the curves for the small ball as well as the large ball do closely mirror each other. Wind tunnels are primary used during aerodynamic analysis of a body. This analysis is done extensively in the automotive and aerospace industry, to try to minimize the drag force by making the design more aerodynamic.
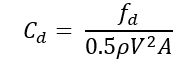
Experimental Results
During the first part of this experiment the wind speed was measured using a Pitot tube. The Pitot tube uses the difference in the static and total pressure to determine the wind speed. The results are listed below in table 1.
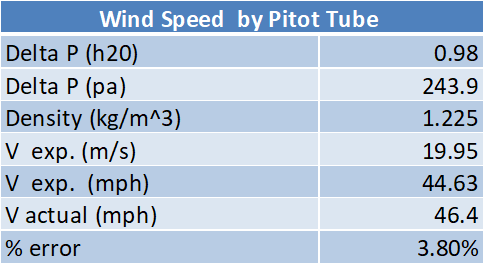
The data of Table 1 was used to create Figure 1, which graphs the Pitot tube Pressure vs the speed in the wind tunnel P(V).
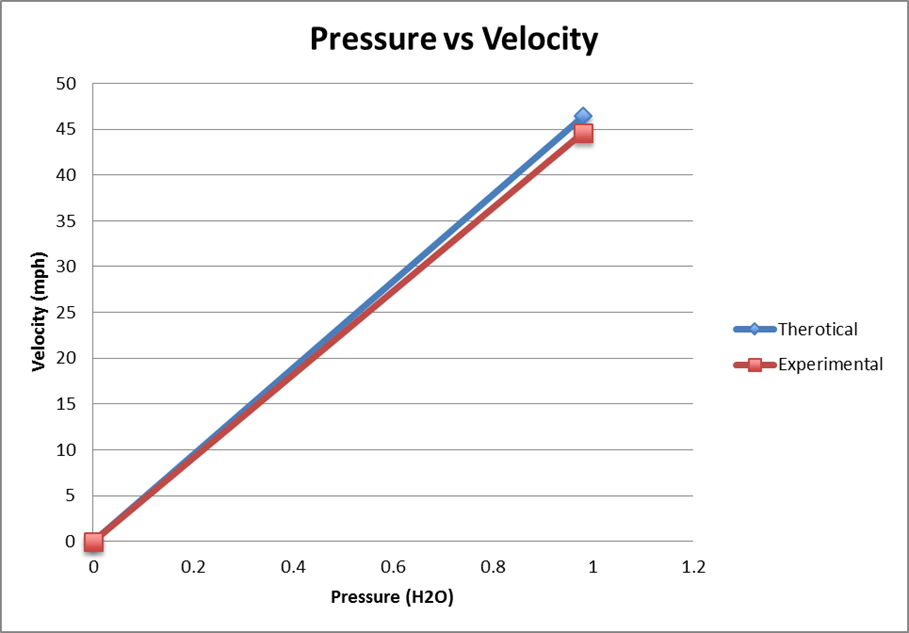
From the graph one can see, there is a linear relationship between Pressure and velocity as the velocity of the wind in the turbine increases so does the pressure measured by the Pitot tube.
During the second part of this experiment two size sphere were placed in the wind tunnel. Table 2; list the data for the small ball with and without a rubber band and Table 3; list the data for the large ball with and without a rubber band.
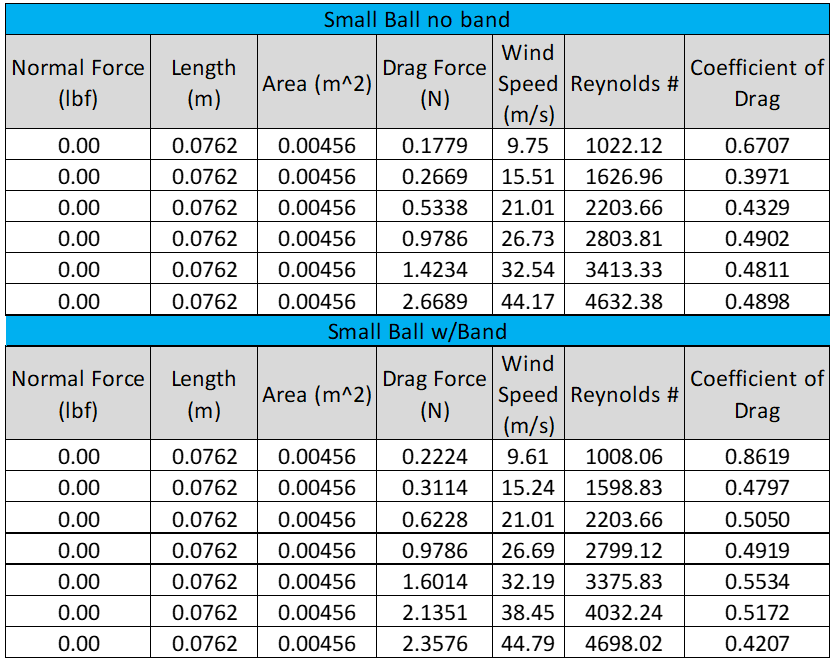
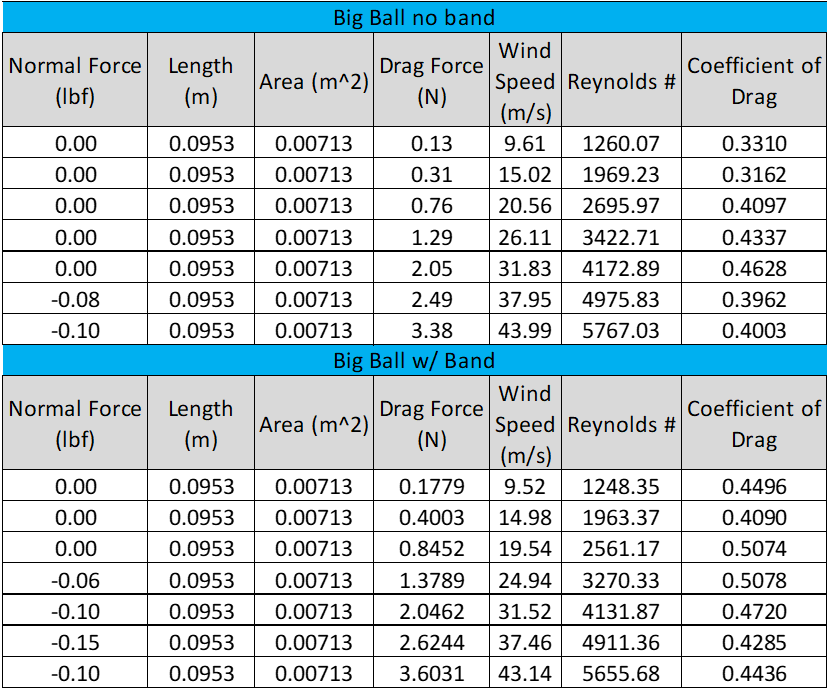
The data from Table 2 and Table 3 was used to create Figure 2, which graphs the drag coefficient as a function of Reynolds number Cd(Re). Each of the 4 scenarios were graphed and trend lines were added with the least square fit to represent this data.
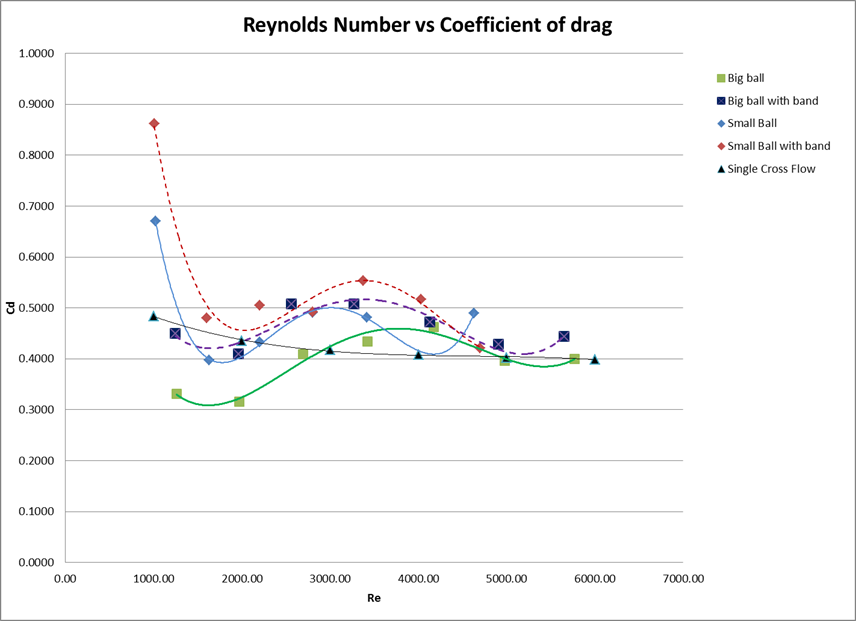
The two solid lines in Figure 2 represent least square fits of the small and large ball without rubber bands. The dashed lines in Figure 2 represent the least square fit for the large and small ball with rubber bands. From the regression analysis of the big ball a statistically significant R2 value of 0.9538 was found for the data set and the line of fit y = 8E-15x4 – 1E-10x3 + 6E-07x2 – 0.0011x + 1.0081 was obtained. Similar results were found the big ball with rubber band with a R2 of 0.8089 and a line of fit of y = 1E-14x4 – 1E-10x3 + 7E-07x2 – 0.0012x + 1.1576. Similar results were found for the small ball with and without the band. The small ball had a R2 value of 0.9989 and a line of fit of y = 5E-14x4 – 6E-10x3 + 2E-06x2 – 0.0043x + 3.0773. Finally the small ball with the band had a R2 value of 0.9722 and a line of best fit of y = 3E-14×4 – 4E-10×3 + 2E-06×2 – 0.0035x + 2.9871. The data set for the single cross flow is represented as a black triangle which was modeled by the equation y = 4E-16x4 – 7E-12x3 + 5E-08x2 – 0.0001x + 0.5904. The statistically significant R2 for each of the regression values support that the coefficient of drag is directly affected by the Reynolds number of the sphere.
Sample Calculations:
Experimental Velocity (m/s):

Convert (m/s) to (mph):
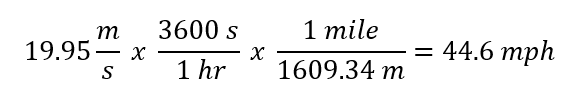
% error:
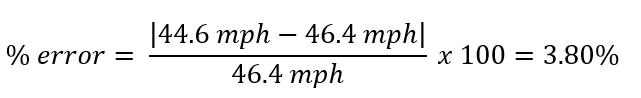
Convert (lbf) to (N):
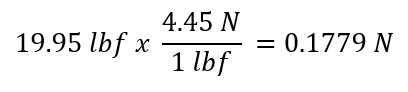
Reynolds Number (-):
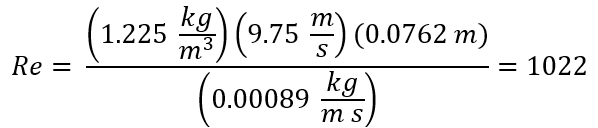
Coefficient of drag (-):

Coefficient of drag singled closed form (-):