Supernode and Supermesh
Today, we’re diving into the fascinating world of circuit analysis. I know it might sound intimidating but fear not! We’re going to unlock the power of two incredible techniques: supernode and supermesh. These tricks will help you simplify those complex circuits and make your analysis journey much easier.
Before we jump into supernodes and supermeshes, let’s quickly understand why circuit analysis is such a big deal. In the field of electrical engineering, analyzing circuits is like peering into the soul of any electronic device. It helps us understand how currents flow, voltages interact, and ultimately, how the entire system behaves. Analyzing circuits can be a real headache, especially when dealing with complex circuits. That’s where supernodes and supermeshes come to the rescue!
Understanding Circuits and Node Analysis
First things first, let’s get familiar with circuits. A circuit is a path that allows electricity to flow, and it consists of various components like resistors, capacitors, and power sources. There are two types of electrical circuits, a series circuit, and a parallel circuit. In circuit analysis, we often deal with nodes, which are points where multiple components connect. Traditional KCL node analysis can get quite messy, as we end up dealing with tons of equations and variables.
How do you define a supernode?
In the realm of circuit theory, a supernode is an abstract concept used to solve a circuit. A supernode is formed when we combine two or more nodes to simplify the analysis. By treating a group of nodes as a single entity, we can reduce the number of equations and variables we need to deal with.
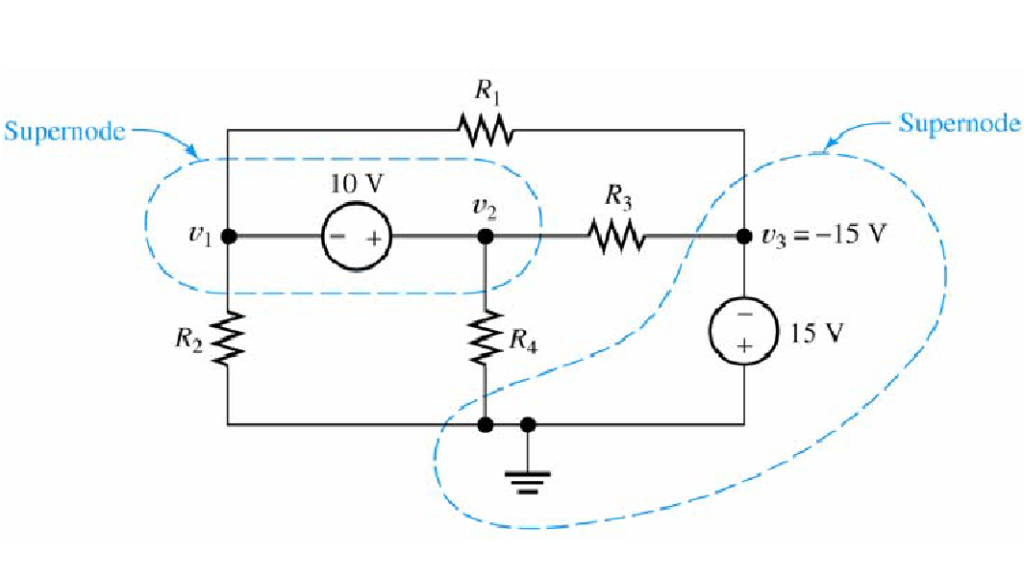
Imagine you have a circuit with multiple nodes, and you want to analyze the currents and voltages. Instead of analyzing each node individually, you can identify a group of nodes that share a voltage source or have the same voltage across them. This group becomes your supernode.

The beauty of a supernode is that you can apply Kirchhoff’s current & voltage law to it just like you would with an individual node. By doing so, you can write a single equation that incorporates the currents and voltages of the components within the supernode. This simplifies the overall analysis and makes it much more manageable.
Can a supernode contain 3 nodes?
A supernode emerges when a voltage source (dependent or independent) is enclosed between two non-reference nodes, along with any components connected in parallel with it. In this scenario, nodes 2 and 3 form a supernode.
Sample problem
To make things clearer, let’s consider an example. Imagine a circuit with multiple nodes connected to resistors and voltage sources. Instead of dealing with each node separately, we can identify a supernode that includes a voltage source and a few connected nodes. By applying Kirchhoff’s laws to this supernode, we can write a single equation that describes the current flowing through the resistors and the voltage across the voltage source. This allows us to solve for the desired parameters without the hassle of analyzing each node individually.
Solutions:
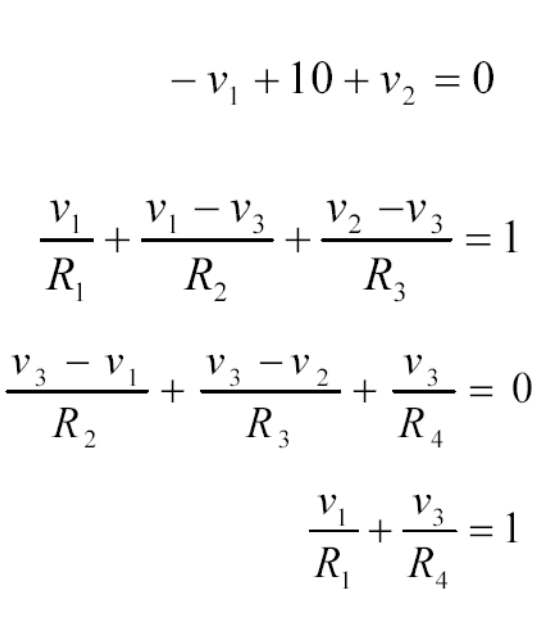
What is the difference between a node and a supernode?
Nodal analysis offers a method for examining electrical circuits by evaluating the voltage at individual nodes relative to a common reference node, typically the ground. Supernode analysis is a specialized technique where two or more nodes are merged into a single node, particularly for nodes that are separated by independent or dependent voltage sources.
What is the use of Supermesh?
Just like a supernode combines multiple nodes, a supermesh combines multiple mesh currents in a circuit. A mesh is a closed loop formed by interconnected components, and we typically analyze them separately. But when we have current sources within two meshes, it can complicate the analysis. That’s where the supermesh comes in!
To form a supermesh, we include the current source within the loop and treat it as part of the mesh. By doing so, we create a simplified analysis by incorporating the current source’s effect directly into the mesh equation. This allows us to solve for the mesh currents without additional equations or variables.
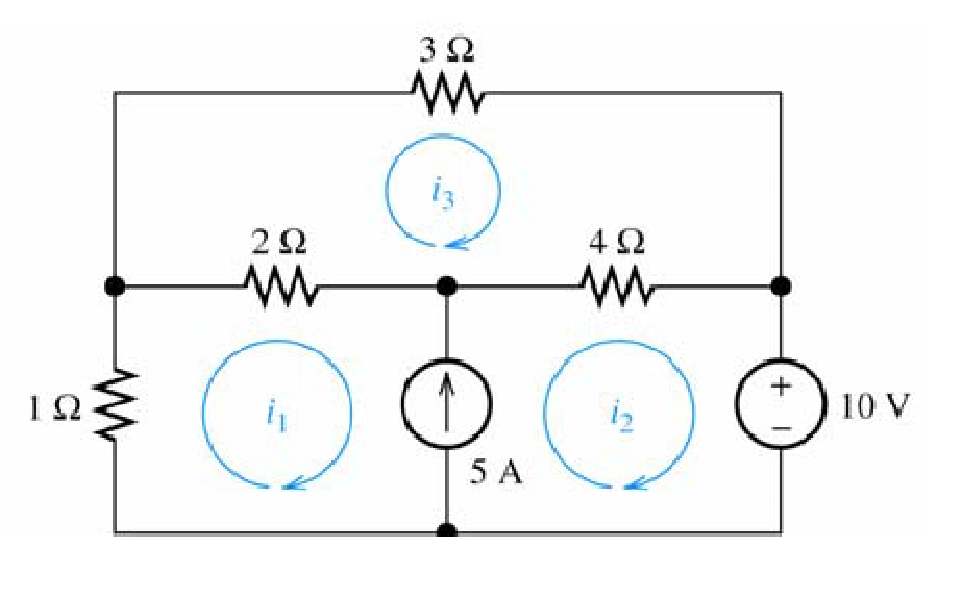
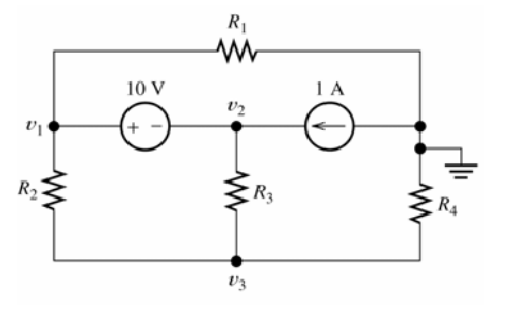
To solve the example above, combine meshes 1 and 2 into a supermesh. in other words, write a KVL equation around the periphery of meshes 1 and 2 combined. A common mistake made by beginning students is to assume that the voltage across the current source is zero.
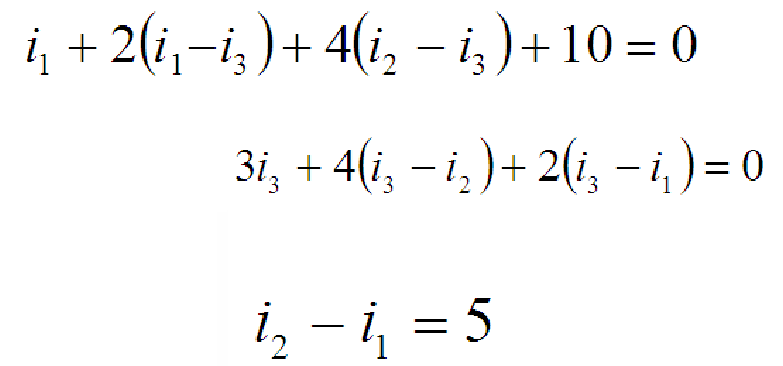
Sample problem
Let’s illustrate this with an example. Imagine a circuit with multiple meshes, each containing resistors and a current source. Instead of analyzing each mesh individually, we can form a supermesh that includes the current source within the loop. By applying Kirchhoff’s voltage law to this supermesh, we can write a single equation that accounts for the voltage source’s effect and the resistors’ currents. This simplifies the analysis and makes it much more efficient.
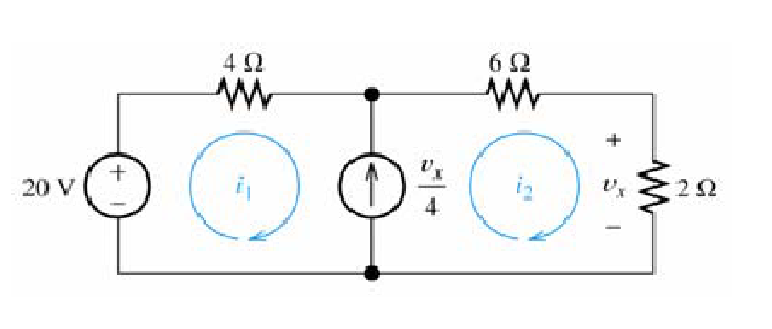
Solution
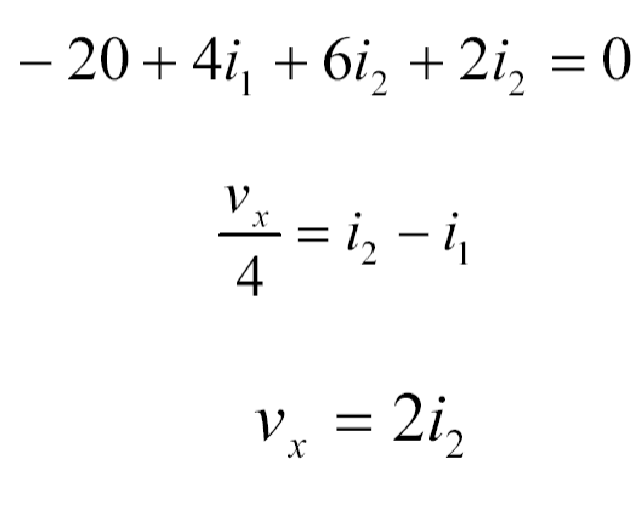
Step-by-Step Guide: Supercharging your Circuit Analysis with Supernode and Supermesh
Now that we understand the power of supernode and supermesh, let’s go through a step-by-step guide to apply these techniques in our circuit analysis:
- Identify the nodes and voltage sources in the circuit: Take a close look at the circuit and identify the nodes, which are the points where multiple components connect. Also, identify the voltage sources present in the circuit.
- Formulate the equations using Kirchhoff’s current and voltage laws: Apply Kirchhoff’s laws to the circuit, writing equations for current conservation at each node and voltage conservation around each loop (mesh).
- Apply the concept of supernode and supermesh to simplify the equations: Identify groups of nodes that can form a supernode, considering voltage sources and shared voltages. Combine the nodes within a supernode and write a single equation that describes the currents and voltages involved. Similarly, identify meshes that can form a supermesh, incorporating current sources within the loop and simplifying the analysis.
- Solve the simplified equations to obtain the desired circuit parameters: With the simplified equations, you can now solve for the currents, voltages, or any other parameters of interest using algebraic techniques or numerical methods.
What is the difference between Supernode and Supermesh analysis?
the difference between supernode and supermesh is that supernodes are employed for nodal analysis in circuits that include voltage sources. Supermeshes, on the other hand, are utilized for mesh analysis in circuits containing current sources. To create a supermesh, identify pairs of meshes that share a branch containing a current source, and combine them into a single loop for analysis.
Conclusion
By leveraging the power of supernode and supermesh, you can supercharge your circuit analysis and make those complex circuits a whole lot simpler. These techniques allow you to reduce the number of equations, variables, and headaches involved in analyzing circuits, making the process more efficient and manageable.
So next time you find yourself facing a daunting circuit analysis task, remember to look for opportunities to apply supernodes and supermeshes. Identify those groups of interconnected nodes or meshes that can be treated as single entities, simplifying the analysis and saving you valuable time and effort.