Kinetics
The Purpose of this experiment was to determine the order of the reaction and how changing the molarity changed the k’ value. To being this experiment 0.2M NaOH concentration was made. Phenolphthalein was then added to the NaOH and the absorbance vs time was recorded. Once all the concentrations were recorded they were plotted to determine they order of the reaction [Concentration vs Time, ln (concentration) vs Time and 1/ln (concentration) vs Time].
If the reaction was a 0 order reaction, then when C vs T was plotted the result would have been a linear line with a negative slope. If the reaction was 1st order then when plotting ln(c) vs T the result would be a negative linear line. Finally if the reaction was second order when plotting 1/ln(c) the result would have been a linear line. The actual results were that the reaction was a 1st order reaction. See Figure 1: ln(c) vs time below.
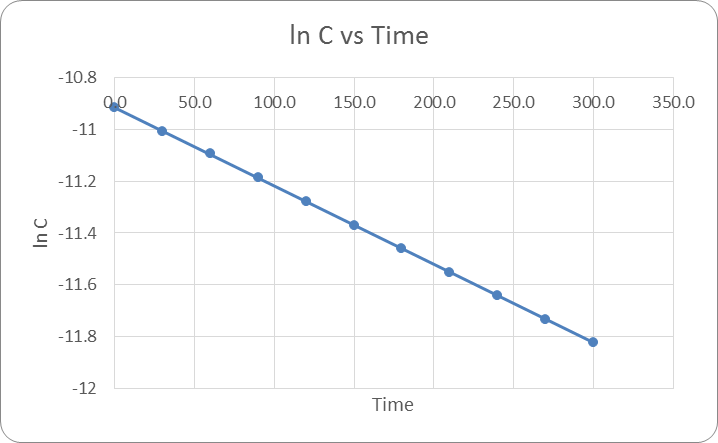
Based on the graph it is apparent that when plotting ln(c) vs time the result is a negative line there for this is a 1st order reaction. The equation of the line was found for each of the three trials and were averaged together. -0.00307x + 10.933 was found to be the average equation.
Based on the average equation the pseudo rate constant was found to be -0.00307 [1/s]. The pseudo rate constants were then found for concentrations of NaOH ranging from 0.150 M -0.30M. These concentration and pseudo rate constants were reordered below. See Table 1: Rate Constant vs Concentration.

The data in table 1 was then graph to be able to determine a relationship between concentration and the rate constant k’. See Figure 2: Concentration vs K’. From this graph it is determined that as the concentration of solution increases so does the k’.
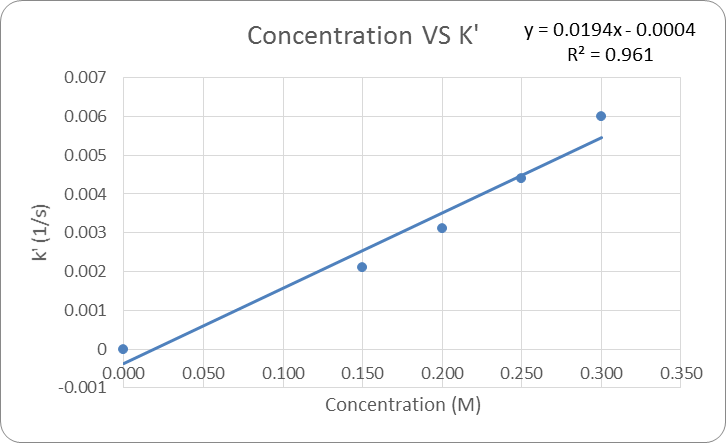
The equation of the trend line for this relationship is y = 0.0194x -0.0004. This equation is y=mx+b form where the slope is the rate for [OH–] and 10intercept is the K constant. Based on this “n” is equal to 0.0194 or about 0.02 and K is equal to 0.999 or about 1. There for the experimental rate equation = (1)[Ind]0.02[OH–]1