Exploring Magnetic Fields and Forces
The interplay between electric and magnetic fields is a cornerstone of classical physics. From understanding the Earth’s magnetic behavior to calculating the torque on a current-carrying loop, magnetic phenomena influence technology and nature.
Earth’s Magnetic Field: A Natural Compass
Earth’s magnetic field, generated by the motion of molten iron and nickel in its core, serves as a shield, protecting the planet from cosmic radiation and charged particles emitted by the Sun. This vast magnetic force behaves as though Earth itself is a giant bar magnet, with its magnetic poles positioned approximately opposite its geographic poles.
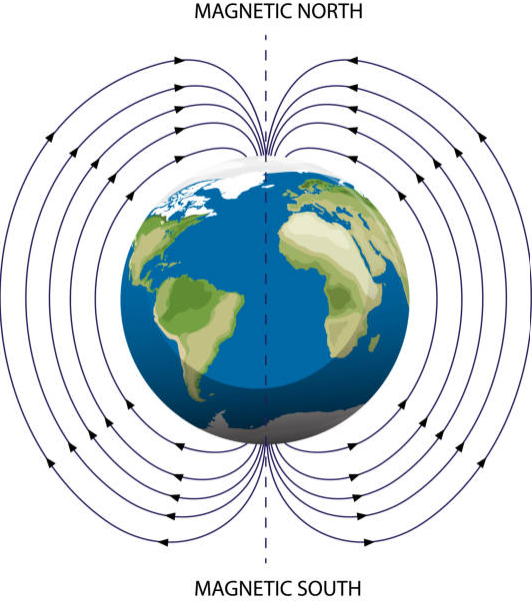
A freely pivoted compass needle aligns with this magnetic field, with its north pole pointing toward Earth’s south geographic pole and vice versa. The Earth’s magnetic field is a vector field, meaning it has both magnitude and direction at any given point in near-Earth space.
The Electric and Magnetic Forces
The electric field (E) is defined by F=qE, and the magnetic field (B) is defined by F=qv×B. The magnetic force F is always perpendicular to both the velocity (v) and the magnetic field (B), following the right-hand rule. For positive charges, F aligns with v×B, and for negative charges, it points in the opposite direction.
The magnitude of F is:
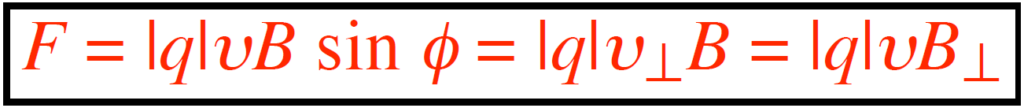
Here:
- F: The magnetic force (in N) on the object
- q: is the object’s charge (Coulombs).
- v: is the object’s velocity (m/s).
- B: the external magnetic field (in T = tesla, where 1 T = 1 N/ A·m ) (Tesla).
This vector equation reveals that:
- The force is perpendicular to both velocity (v) and the magnetic field (B).
- The magnitude depends on charge, speed, and the angle ϕ between v and B: F=∣q∣vBsinϕ
- F=0: When v is Parallel (ϕ=0 degree) or antiparallel (ϕ=180 degree).
- F is maximized: When v is (ϕ=90 degree) to B.
If the only interaction for a charged particle is the qυ× B magnetic force, its speed remains constant.
Magnetic Field Lines
Magnetic field lines help visualize the field:
- The direction of B at any point is tangent to the field line.
- Field strength is proportional to the density of lines.
- Lines form closed loops, indicating no isolated magnetic poles (monopoles).

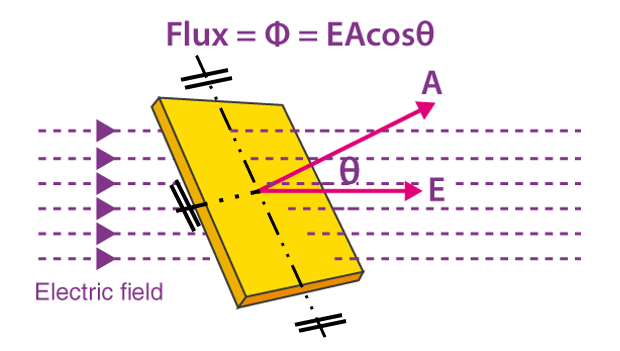
Magnetic Flux and Gauss’s Law
Recall that we define the electric flux ΦE by ΦE ≡ ∫E·dA. Similarly, we define the Magnetic Flux (ΦB)
by:

f the magnetic field is uniform and the surface is flat, we can pull the constants out of the integrals to obtain:
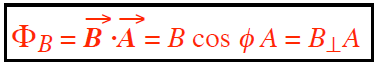
Units: ΦB is magnetic flux (in Webers (Wb), where 1 Wb=weber = 1 tesla·(meter)2 = 1 T·m2 )
Gauss’s Law for Magnetism: The net magnetic flux through any closed surface is zero:
∫B⋅dA=0
This is true because there are no N-poles or S-poles by themselves, that is, no magnetic monopoles.
Magnetic Force on Current-Carrying Wires
A straight wire in a uniform magnetic field experiences a force given by:
F=ILBsinϕ =ILB⊥
Where:
- F: is the magnetic force (in N) on the wire: nonzero F is always perpendicular to both I and B.
- I: is the current (in A) in the wire
- L: Length of the wire (in m) of the straight-wire segment (with the direction that the current flows).
- B: is the uniform external magnetic field (in T)
- ϕ: Angle between the wire and the magnetic field.
If ϕ=90 degrees, the force is maximized; if ϕ=0 or 180 degrees, the force is zero.
If the wire is not straight and/or the magnetic field is not uniform, we can find the magnetic force by
performing a vector integral of dF= I dL× B
Lorentz Force Law:
This principle states that the force on a current-carrying wire in a magnetic field is proportional to the current (I), the length of the wire (L), and the magnetic field strength (B). This force is perpendicular to both the current direction and the magnetic field. A coil with n turns of wire will produce n times the amount of current when pivoted at one end.
F=nBIL
Magnetic Dipoles and Torque
Magnetic Dipole: A current loop forms a magnetic dipole with a magnetic moment μ=NIA (where μ is the magnetic dipole moment (in A·m2) N is the number of turns (no unit), I is the current (in A), and A is the loop area (in m2)). The right-hand rule gives the direction of μ.
τ=NIABsinϕ and μ=NIA give us the magnitude of the torque.
Torque: In a uniform magnetic field B, a dipole experiences no net force but does experience torque:
τ = μB sin φ
Where:
- τ: is the magnetic torque (in N·m): a nonzero τ is always perpendicular to both μ and B
- B: is the external magnetic field (in T).
- φ: is the angle between the directions of the two vectors μ and B; 180° ≥ φ ≥ 0.
The dipole moment (μ=NIA) aligns with the field, reducing magnetic potential energy (in J) :

The Hall Effect
When a current-carrying conductor is placed in a transverse magnetic field, a potential difference arises across the conductor. This phenomenon, the Hall Effect, is crucial in modern sensors and measurement devices.
Applications of Magnetic Fields
Magnetic fields have numerous applications across various fields, playing a crucial role in technology, medicine, industry, and environmental management:
Medical Applications
- Diagnosis and Imaging: Magnetic fields power diagnostic tools like Magnetic Resonance Imaging (MRI) and Magnetic Resonance Tomography (MRT), which visualize physiological processes.
- Therapeutic Uses: They are employed in treating cancer, hyperthermia, inflammation, and gastrointestinal disorders, and in adjusting blood flow during surgeries.
- Drug Delivery: Magnetic nanoparticles assist in targeted drug delivery and stem cell therapy.
- Hyperthermia Therapy: Alternating magnetic fields are used to kill cancer cells.
Industrial and Engineering Applications
- Fluid Dynamics and Heat Transfer: Magnetic fields modify the properties of electrically conducting fluids, benefiting operations like metallurgical processing and magnetic stirring.
- Magnetohydrodynamics (MHD): Applications include MHD generators, accelerators, and pumps in energy and industrial processes.
- Nanotechnology: Magnetic fields aid in manipulating nanofluids and optimizing heat transfer in thermal engineering.
Biotechnology
- Biosensors and Biochips: Magnetoresistive-based devices detect biological events, enhancing biosensing and diagnostics.
Environmental and Agricultural Applications
- Water Treatment: Magnetic treatment technology improves water purification processes.
- Agriculture: Magnetic fields enhance agricultural processes for better resource efficiency.
These applications underscore the versatility of magnetic fields in improving healthcare, driving technological innovation, and addressing environmental challenges.
Conclusion
Magnetic fields and forces are fundamental to understanding the physical world and enabling modern technologies. From their role in natural phenomena like Earth’s magnetic field to their applications in medicine, industry, and environmental science, magnetic forces profoundly influence our lives.
We gain insights that drive innovation by exploring concepts such as the Lorentz force, magnetic dipoles, and the interactions between current and magnetic fields. Whether in the design of electric motors, advancements in medical imaging, or environmental applications, the study of magnetic fields continues to unlock new possibilities, shaping the future of science and technology.