Understanding Moment of Inertia

Physics often focuses on simplifying complex phenomena to better understand and predict the natural world. This art of idealization is a cornerstone of mechanics, where we frequently encounter the concept of a “particle” or “point mass.” Within this context, the moment of inertia plays a crucial role, particularly in rotational dynamics.

In thermodynamic equilibrium, all physical objects exhibit positive moments of inertia, indicating that to initiate the rotation of a stationary object, a torque must be applied. However, while negative moments of inertia are impossible under thermal equilibrium, they can occur in non-equilibrium, open systems.

Moment of Interia: Point mass calculation

Point Mass and Standard Units

In physics, when we deal with rotational motion, we often simplify objects to point masses to make calculations manageable. The units used in these calculations are typically from the International System of Units (SI): meters (m) for distance, kilograms (kg) for mass, and seconds (s) for time. This idea allows us to disregard the size or structure of an object in a given problem, treating entities like electrons or planets as singular points.

Point mass Example

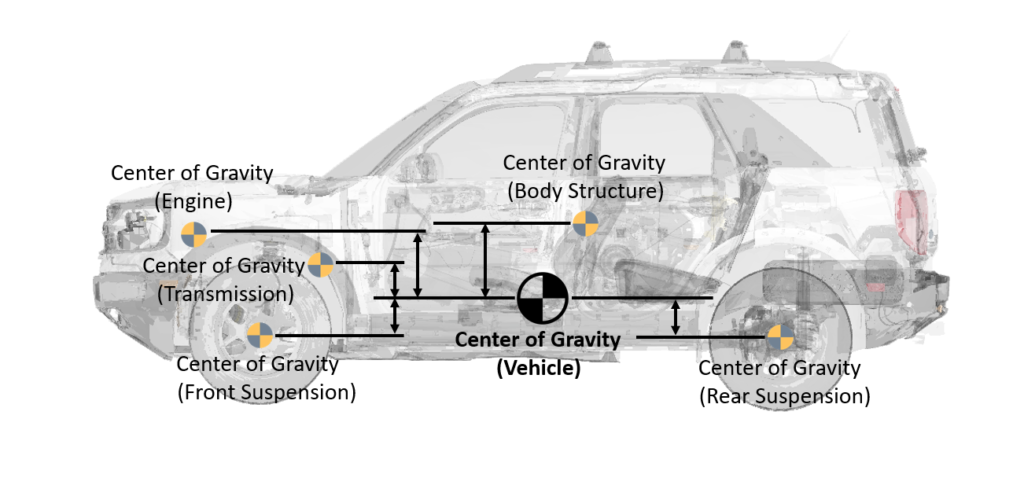
Using Point mass to calculate the moment of inertia of a whole vehicle

When determining the moment of inertia of a vehicle, you can simplify the process by treating all major subsystems of the vehicle as point masses. This approach transforms the problem into a point mass calculation, where you compute the moment each subsystem exerts on the distance from the axis of rotation (vehicle’s center of gravity). By doing so, you can significantly simplify the problem, avoiding the need to calculate the center of gravity for each specific component.

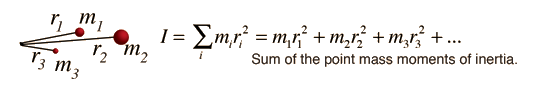
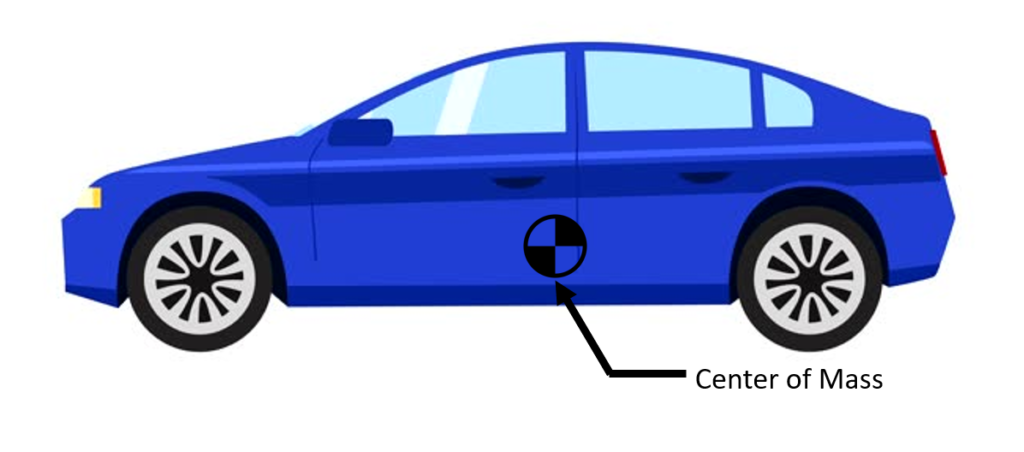
Moment of Interia: Multiple Point mass calculation

Center of Gravity

The center of gravity of an object is the point where its entire weight can be considered to be concentrated. This point is also known as the center of mass. For symmetric and homogeneous bodies, the center of gravity lies along the axis of symmetry.

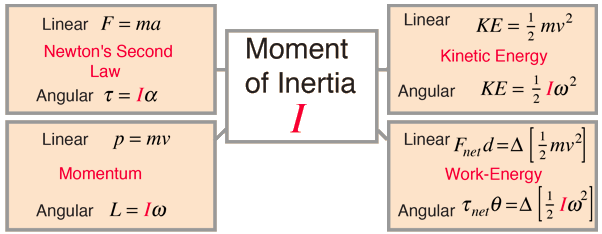
What is a Moment of Inertia?

In simple terms, the moment of inertia measures the amount of torque needed for a specific angular acceleration about a rotational axis. It can be thought of as the rotational equivalent of mass in linear motion. The units of the moment of inertia are kg⋅m² or g⋅cm².

In more technical terms, the moment of inertia (I) quantifies the resistance a body exhibits to changes in its rotational speed about an axis. This axis can be internal or external and fixed or variable. It is defined as the sum of the product of the mass of each particle and the square of its distance from the axis of rotation.

What is the difference between I_x and Iy?

The difference between I_x and I_y lies in the axis about which the moment of inertia is measured.

Ix refers to the moment of inertia about the x-axis, also known as roll inertia. This measures how much an object resists rotational motion around the x-axis, which typically corresponds to rolling movements in an object.
Iy refers to the moment of inertia about the y-axis, also known as pitch inertia. This measures the resistance to rotational motion around the y-axis, which is associated with pitching movements, such as a vehicle tilting forward or backward.

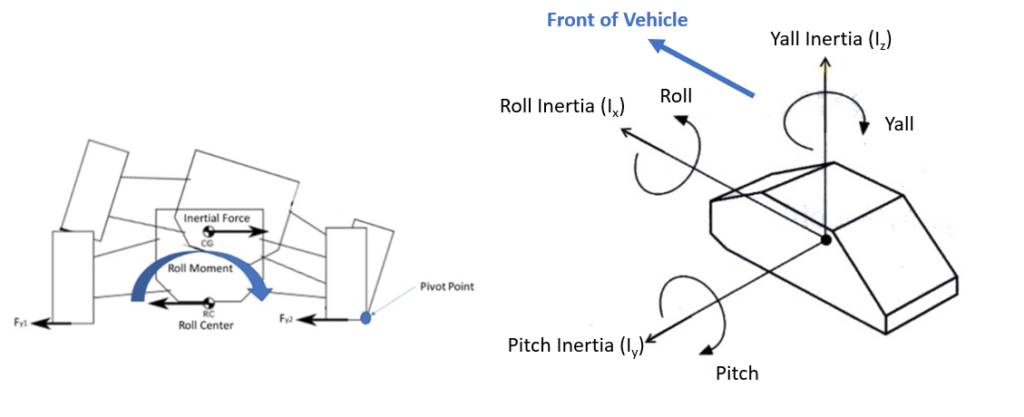
Moment of Interia (Roll, Pitch, and Yall)

In summary, I_x is concerned with roll, while I_y is concerned with pitch.

How is the moment of inertia calculated?

The moment of inertia, I_x, is determined by summing the products of all elemental areas located above or below the centroid x-axis of the cross-section, each multiplied by the square of the distance from the centroid of each element to the centroid of the entire cross-section.

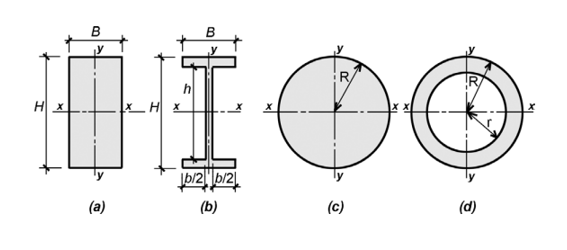
Cross sections typically encountered as structural elements include (a) rectangles, (b) I-shaped sections, (c) circles, and (d) circular rings

Here, y represents the distance from each elemental area dA=width×dy to the centroid of the cross-section. The limits H/2 and -H/2 define the range over which the integral is calculated for both the rectangular and I-shaped sections, and this equation applies in the same way to each section.

Torque and Moment of Inertia

Torque 𝜏 is the rotational equivalent of force. It is defined as the product of the tangential force F_t and the radius r of the rotation object. Mathematically, τ=F_t⋅r. Given that F_t = ma_t, where a_t is the tangential acceleration, and knowing that a_t = r⋅α where α is the angular acceleration), we get:

𝜏= m⋅r²⋅α

Here, (m⋅r²) is defined as the moment of inertia (I).

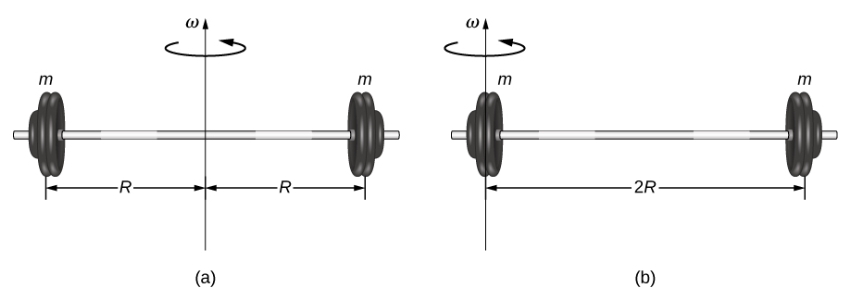
Moment of Interia Example

When the axis is positioned in the center of the barbell, each of the two masses ( m ) is at a distance ( R ) from the axis, resulting in a moment of inertia calculated as I_a=mR²+mR²=2mR². Conversely, when the axis is located at the end of the barbell—passing through one of the masses—the moment of inertia is given by I_b=m(0)²+m2R²=4mR². This outcome shows that it is twice as difficult to rotate the barbell about its end than it is about its center.

Kinetic Energy of Rotation and Rotational Inertia

The kinetic energy of a rotating object is given by the formula:

K = 0.5Iω²

Where ( I ) is the moment of inertia and (ω) is the angular velocity. This formula applies to both point masses and solid bodies rotating about an axis.

Examples of Moment of Inertia Calculations

Collection of Point Masses:

For two identical masses (m) at x=±a/2 rotating in the xy plane about the z-axis through the center of mass:
I=2⋅m (a/2)²=(ma²) /2

Hoop:

A hoop of mass (M) and radius (R) rotating about its central axis:
I = MR²

Example 7 Moment of Inertia of a Hoop

Find the moment of inertia of a hoop of mass M and radius R about an axis that is perpendicular to
the plane of the hoop and goes through its center. Derive an expression for J in terms of M
and the hoop geometry (radius).

Rod:

A uniform rod of mass (M) and length (L) rotating about its center:
I=(ML²)/12

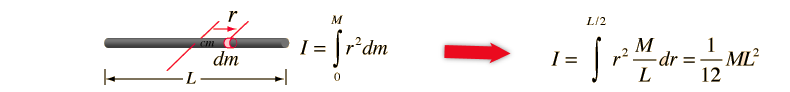
Derivation of Rod Momment of interia calculation

Disk:

A uniform disk of mass ( M ) and radius ( R ) rotating about its center:
I=1/2 (MR²)

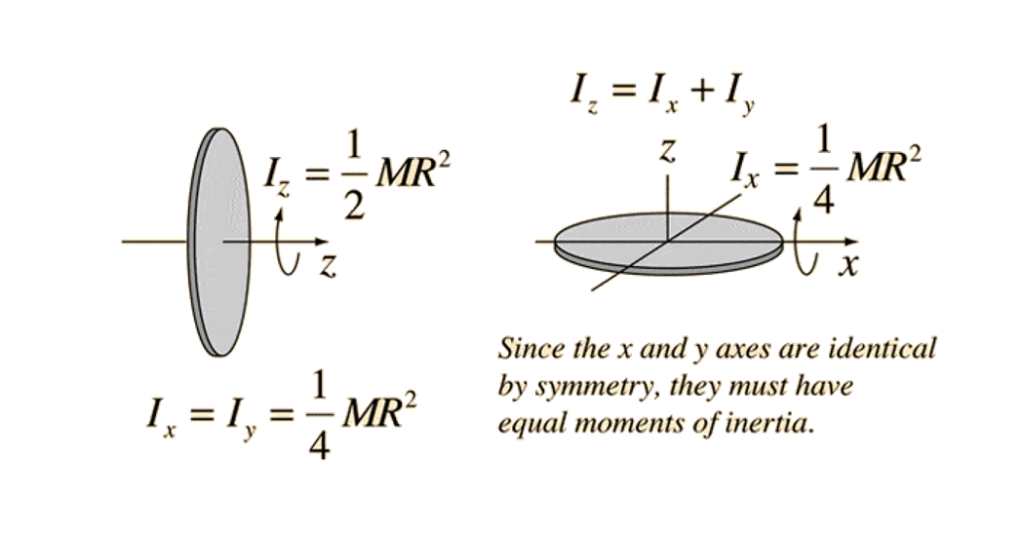
Solid Sphere:

A solid sphere of mass ( M ) and radius ( R ) rotating about its center:
I=2/5 (MR²)

Hollow Sphere:

A hollow sphere of mass ( M ) and radius ( R ) rotating about its center:
I=2/3 (MR²)

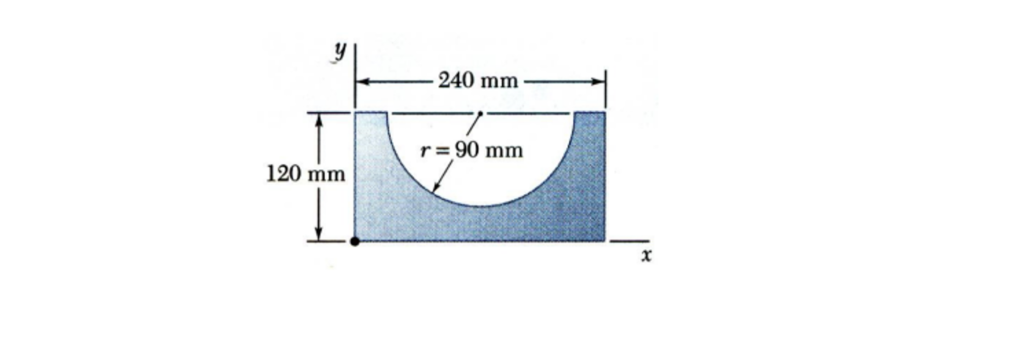
Sample Problem

Determine the moment of inertia of the shaded area concerning the x-axis.

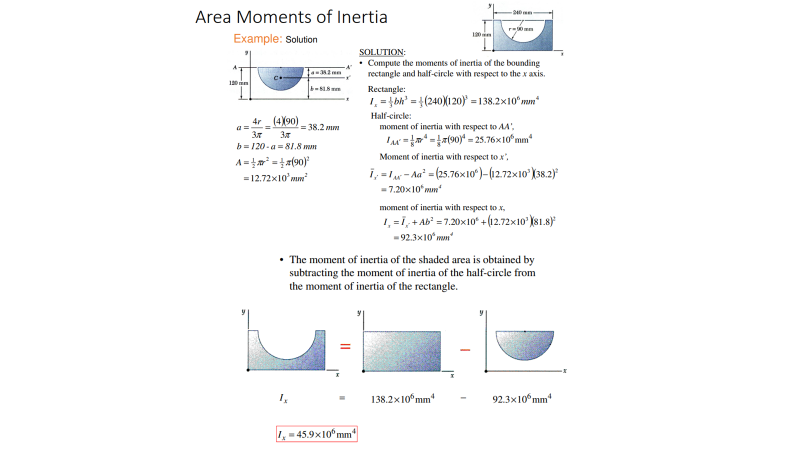
Solution

Parallel Axis Theorem

The parallel axis theorem is used to calculate the moment of inertia about any axis parallel to the axis through the center of mass. It is given by:

I=I_cm+MD²

Where (I_cm) is the moment of inertia about the center of mass axis, (M) is the mass of the body, and (D) is the distance between the two axes.

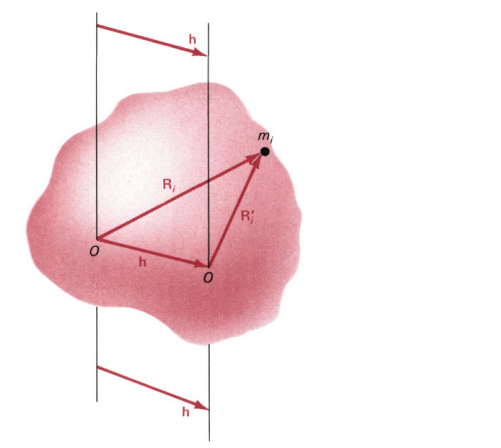
Two axes are shown perpendicular to the lamina. One axis intersects the lamina at O and the other axis intersects the lamina at the center of mass at Or. The two axes are
separated by the vector displacement h. A mass m has the
radius vectors R, and R/, respectively, relative to the two axes.

Significance of Moment of Inertia

A higher moment of inertia indicates that more force is required to achieve the same angular acceleration, meaning the body is more resistant to changes in its rotational motion. Conversely, a lower moment of inertia means the body is easier to rotate. This concept is vital in various applications, from designing efficient machinery to understanding the dynamics of celestial bodies.

Why is the moment of inertia important?

The moment of inertia is crucial because it quantifies an object’s resistance to changes in its rotational motion. This property is vital for understanding and predicting how much torque (rotational force) is needed to alter an object’s angular velocity. MOI is fundamental in various applications, particularly in vehicle dynamics and control systems.

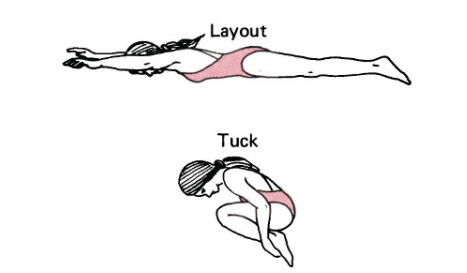
Example of Moment of inertia in real life

When a diver transitions from the layout position to the tuck position, she alters her moment of inertia, potentially reducing it by a factor of seven. There are numerous instances where a body can be considered rigid both before and after internal forces modify its moment of inertia relative to the center of mass. However, during this transformation, the body is not rigid, and the moment of inertia is not constant.

A diver is shown in the layout and tuck positions.

How does the moment of inertia affect vehicle dynamics?

The moment of inertia plays a crucial role in determining how a vehicle responds to various driving conditions, impacting its handling, acceleration, ride comfort, and braking performance. Understanding and accurately estimating the vehicle’s inertial properties are essential for achieving optimal comfort, safety, and fuel efficiency. Additionally, a moment of inertia affects the responses of moments and acceleration, highlighting its significance in vehicle dynamics.

Conclusion

The moment of inertia is a fundamental concept in rotational dynamics, providing a measure of an object’s resistance to changes in its rotational motion. By understanding and calculating the moment of inertia, we can better predict and control the behavior of rotating systems, making it an essential topic in physics and engineering.