Electric Potential and Energy

Hey everyone! Today, we are going dive into the fundamental concepts from Physics 2, covering electric potential, energy, and the relationships governing charged particles. These principles are crucial for understanding electrostatics and provide a foundation for advanced applications in physics and engineering.

What is meant by electric potential energy?

Okay, so first things first – what exactly is electric potential energy (also known as electrostatic potential energy)? Electric potential energy refers the energy that is needed to move a charge against an electric field. This attraction or repulsion between charges is related to their positions relative to one another. Changes in potential energy can lead to electrical work and various electrical phenomena.

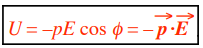
where U is the electric potential energy (in J = joule). Energy is a scalar quantity, so U has no direction. (we use p = |q|r rather than p = qd).

What is the derivation of electric potential energy equation?

Revisiting the relationship from General Physics I, the work W_a→b done by a force F in moving a particle from point a to point b is defined to be

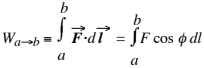
If the force is conservative, W_a→b = U_a – U_b, where U is the potential energy associated with that force.
If we have a test charge q₀ outside a spherically-symmetric, same-sign charge q,

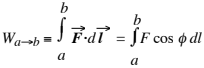
,where

and dl cos φ = dr. Then integrating from r_a to r_b gives us

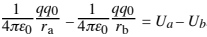
Thus the simplest choice for the potential energy expression is

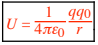
This equation also holds for opposite-sign charges. Any equation in this block containing ε₀ is for vacuum ≈ air. is the electric potential energy (in J). Recall that 1/4πε₀= 8.988 × 10⁹ N·m² /C² ≈ 9.0 × 10⁹N·m² /C²

q and q₀ are the charges (in C)—(point or spherically symmetric) (recall that charges can be +, 0, or –). r is the center-to-center distance (in m) between the two charges (recall that r is always +). Thus we see that U is + for same-sign charges and – for opposite-sign charges. We also see that U approaches zero as the distance r approaches infinity. This U can be used in K_a + U_a = K_b + U_b (W_other = 0).

Key takeaways:

• U>0 for same-sign charges, U<0 for opposite-sign charges.
• As r→∞, U→0.

Electric Potential (V)

The (electric) potential V at a point is the electric potential energy per charge at that point, V =
U/q₀. Therefore, dividing both sides of W_a→b = U_a – U_b by q₀ tells us that the work per charge
W_a→b/q₀ is the (electric) potential difference V_a – V_b between points a and b :

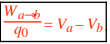
We often shorten V_a – V_b to V_ab (and for electric circuits, often further to just V). V is the (electric) potential (in V = volt = joule/ coulomb = J /C ) (V can be +, 0, or –). W_a→b is the work done (in J) by the external electric field in moving q₀ from a to b (W_a→b can be +, 0, or –).

For a point charge q (or outside a spherically symmetric charge q) we can substitute

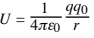
to find

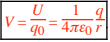
For a collection of these charges,

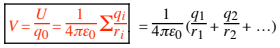
q_i is the charge (in C) of object i (qi is +, 0, or –). r_i is the distance (in m) from the center of object i (r_i is always +). For a continuous charge distribution,

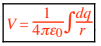
That is, first find an expression for the dV from an arbitrary dq in the distribution, then integrate to find V Finding V_a – V_b from E : Recall that

Canceling out q₀, we have an equation we can use to find the potential difference if we know E all along any path from a to b.

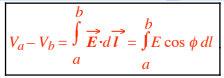
we’ll replace dl with dx or dy or dz, or dr in the integral. Note that E can have units of either V/m or N/C : 1 V/m = 1 (J/C)/m = 1(N·m/C)/m = 1N/C .

Key concepts:

• V is measured in volts (1 V=1 J/C).
• V can be positive, negative, or zero depending on charge distribution and sign.

Equipotential Surfaces: Key Insights and Characteristics

The term equipotential refers to a region where the electric potential V remains constant. This can apply to points along an equipotential line, across an equipotential surface, or within an equipotential volume.

Equipotential surfaces play a crucial role in understanding electric fields and potentials. These surfaces help visualize the distribution of electric potential in a given space and provide valuable information about the behavior of electric fields.

Definition

An equipotential surface is a three-dimensional surface where every point has the same electric potential V. Since potential is constant across the surface: V_a−V_b=0 for any two points  a and b on the surface.

Electric field lines are always perpendicular to equipotential lines or surfaces. When free charges on a conductor are in electrostatic equilibrium, the conductor’s surface becomes an equipotential surface, with the electric field at the surface oriented normal to it. Additionally, within an equipotential volume, where the potential remains constant, the electric field E is zero, as indicated by E⃗=−∇V , since the gradient of a constant is zero.

What is an example of electric potential energy in real life?

Some of the most common examples of electrical potential energy is when you rub a balloon on your hair and it sticks to a wall, that’s a bit of electric potential energy in action. Weird, right? But cool! The same thing happens when you shuffle your feet on a carpet and get a little zap when touching a metal doorknob.

Basically, it’s all about how charges build up. Like, imagine positive and negative charges as tiny teams of cheerleaders. When they get together on one side of the balloon or your body, they’re like, “Woohoo, we’ve got potential energy!” And when they finally get the chance to jump from the balloon or you to the wall or doorknob, they release that energy in the form of a little electric shock.

Voltage: The Driving Force

Now, let’s talk about voltage. Think of it as the pressure pushing those charges around. It’s like water pressure in a hose – the higher the pressure, the stronger the flow. So, when we talk about high or low voltage, we’re talking about how eager those charges are to move and do their thing.

In the world of electrical systems, voltage is a big deal. It’s what makes electricity move from place to place, just like water flows through a pipe. Without voltage, all those electrical devices we love would be just expensive paperweights!

Electron Volt: A Practical Energy Unit

One electron volt (eV) is defined as the work done in moving a single electron through a potential difference of one volt:1 eV=1.602×10⁻¹⁹ J

How is voltage related to potential energy?

Voltage is directly related to potential energy in electrical systems. Voltage represents the amount of energy carried by electric charges per unit of charge, measured in joules per coulomb ( = volts). The Higher the voltage means the greater the potential energy. The greater the potential energy driving charges to move and more “work” can be done, while lower voltage indicates less energy available for electrical devices and circuits.

How Electric Potential Energy Moves

Alright, now you might wonder how this electric potential energy actually moves. The secret lies in conductors and insulators. Conductors are like the superstar carriers of electric charge; they allow electricity to flow through them with ease. Copper wires are a classic example of conductors.

On the other hand, insulators are like the bodyguards of charge; they keep it contained and don’t let it escape. Rubber is a great insulator, which is why electrical cords have rubber coatings.

That’s where closed circuit come into play. A closed electrical circuit is like a never-ending “Ring Around the Rosie” game. The charges can keep going round and round, allowing electricity to flow continuously, powering our gadgets and appliances.

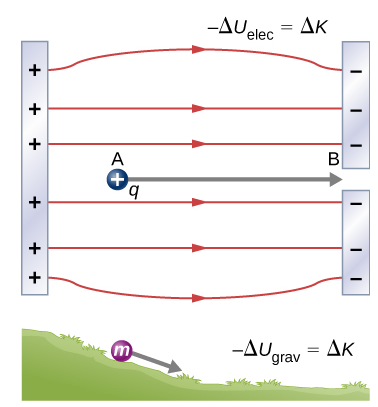
What is work in an electric field?

In an electric field, work refers to the energy transfer that occurs when a charged particle moves between two points with different electric potentials. If the particle moves in the direction of the electric field, work is done by the electric field, increasing the particle’s kinetic energy. Conversely, moving against the electric field requires work to be done on the particle, reducing its kinetic energy.

Why is the electric field stronger at sharp points of a conducting surface, and how does this affect electrical discharge?

The electric field from a charged conducting surface tends to be greatest where the radius of curvature is smallest (for sharp points and thin wires). This large electric field can break down the air, giving an electrical discharge. In contrast, flatter areas tend to have smaller surface electric fields. Finding E from V:

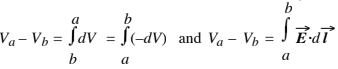
tells us that –dV = E*dl. Evaluating the scalar (dot) product in terms of components gives –dV = E_xdx + E_ydy + E_zdz. Keeping both y and z constant gives dy = 0 and dz = 0, so –(dV/dx )y,z constant = E_x. Such a derivative is called a partial derivative and we have:

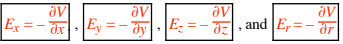
E_x is the x-component of the electric field E (in V/m or N/C) (with the same idea for y, z, or r) . Then E = E_x i+ E_y j+ E_z k= –( i ∂/∂x + j ∂/∂y + k∂/∂z )V. The quantity in the parentheses is the gradient operator ∇ , so E = – ∇ V. In words, the electric field equals the negative of the potential gradient

Practical Applications of Electric Potential Energy

Alright, let’s talk about the juicy stuff – how electric potential energy affects our lives. Remember when we talked about how it powers your smartphone? Oh yeah, that little device is like a tiny powerhouse, thanks to electric potential energy. Every time you charge it up, those charges are getting all pumped up with energy, ready to keep your phone running throughout the day.

 Electric potential energy is crucial in the development and functioning of batteries, supercapacitors, and fuel cells, which are essential for energy storage and supply. Techniques such as photovoltaic systems for solar energy and turbines for wind energy utilize electric potential energy to convert natural energy into usable electric power

Also think about those massive industrial machines that create everything from cars to the packaging of your favorite snacks. Yep, electric potential energy is at work there too, making sure everything runs smoothly and efficiently.

Problem-Solving Tips

• Start with general equations and apply boundary conditions or symmetry.
• For continuous charge distributions, break the problem into infinitesimal elements dqdq, then integrate.
• Use gradients to find electric fields from known potentials.

---

By mastering these concepts, you’ll unlock a deeper understanding of electrostatics and their implications in fields like circuit design, electromagnetism, and beyond. Stay tuned for more physics insights!

Class Notes