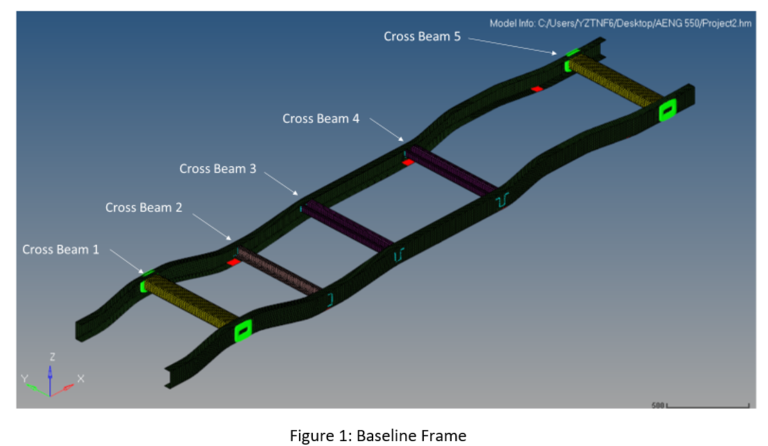
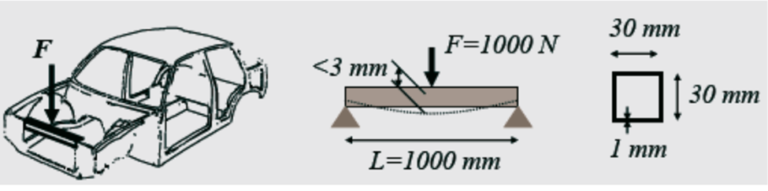
Roll Control System Simulation
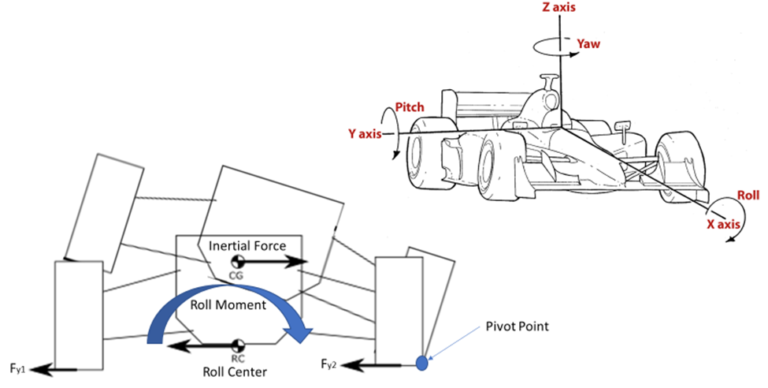
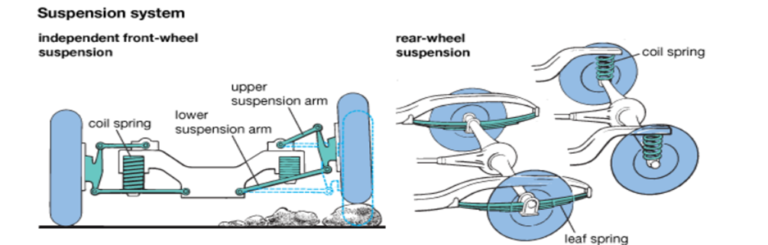
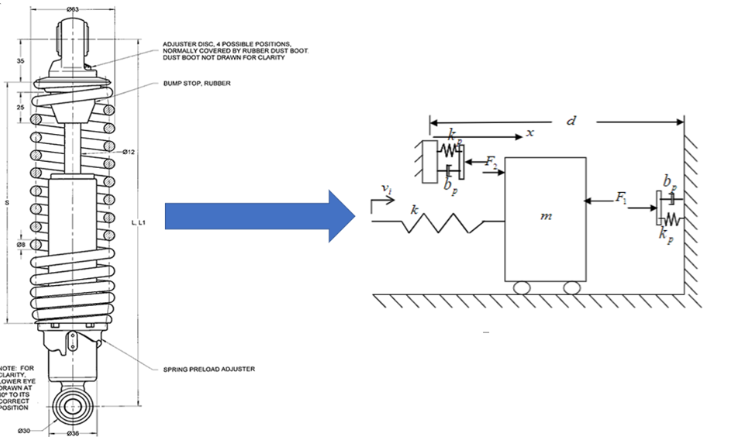
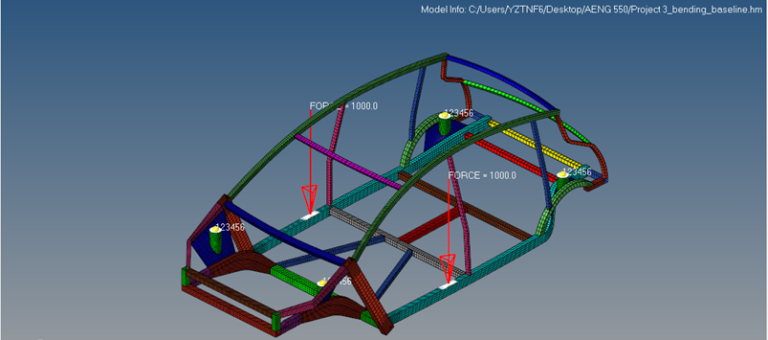
This simulation is of a vehicle performing a cornering maneuver. During a cornering maneuver, the rolling motion or roll angle which is felt in the vehicle about the x-axis is a result of the inertial forces acting on the vehicle’s center of gravity and the vertical elasticity of the suspension. The roll axis is the…