Month: January 2022

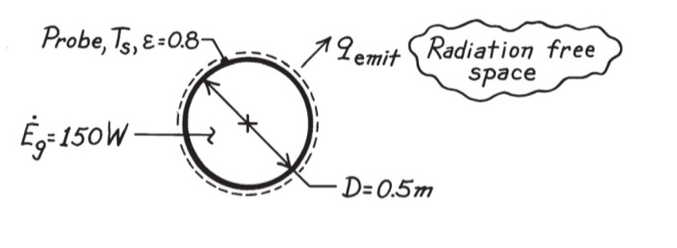
A spherical interplanetary probe of 0.5-m diameter contains electronics that dissipate 150 W. If the probe surface has an emissivity of 0.8 and it does not receive radiation from other surfaces, such as the sun, what is the surface temperature of the probe?

The 5-mm-thick bottom of a 200-mm-diameter pan may be made from aluminum (k = 240 W/m·K.) or copper (k = 390 W/m·K.). When used to boil water, the surface of the bottom exposed to the water is nominally at 110 °C. If heat is transferred from the stove to the pan at a rate of…

A glass window of width W= 1 m and height H = 2 m is 5 mm thick and has a thermal conductivity of kg 1.4 W/m·K. If the inner and outer surface temperatures of the glass are 15°C and -20°C, respectively, on a cold winter day, what is the rate of heat loss through…

The thermal conductivity of a sheet of rigid, extruded insulation is reported to be k = 0.029 W/m·K, the measured temperature difference across a 20mm-thick sheet of the material is T1-T2 =10°C. (a) What is the heat flux through a 2m x 2m sheet of insulation? (b) What is the rate of heat transfer through…

Consider the geometry of Problem 2.14 for the case where the thermal conductivity varies with temperature as k = ko + aT. where ko = 10W/m-K, a =-10-3 W/m-K2, and T is in kelvins. The gradient at surface B is partial differential T/partial differential x = 30 K/m. What is partial differential T/partial differential y at…

To determine the effect of the temperature dependence of the thermal conductivity on the temperature distribution in a solid, consider a material for which this dependence may be represented as k = ko + aT where ko is a positive constant and a is a coefficient that may be positive or negative. Sketch the steady-state…

Assume steady-state, one-dimensional heat conduction through the symmetric shape shown. Assuming that there is no internal heat generation, derive an expression for the thermal conductivity k(x) for these conditions: A(x) = (1 – x), T(x) = 300(1 – 2x – x3), and q = 6000 W, where A is in square meters, T in kelvins,…